勾股定理證明最簡單的方法

勾股定理現約有500種證明方法，是數學定理中證明方法最多的定理之一。那么勾股定理證明最簡單的方法有哪些呢？下面就和小編一起了解一下吧，供大家參考。

勾股定理證明有什么簡單的方法

證法一：

這是最簡單精妙的證明方法之一，幾乎不用文字解釋，可以說是無字證明。如圖所示，左邊是4個相同的直角三角形與中間的小正方形拼成的一個大正方形。

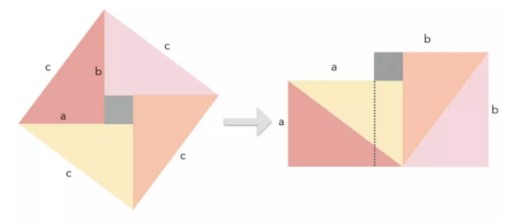
圖形變換后面積沒有變化，左邊大正方形的邊長是直角三角形的斜邊c，面積是c2；右邊圖形可分割為兩個正方形，它們的邊長分別為直角三角形的兩條直角邊a和b，面積就是a2＋b2，于是a2＋b2＝c2。

圖中左邊的“弦圖”最早出現在公元222年的中國數學家趙爽所著《勾股方圓圖注》，趙爽是我國數學史上證明勾股定理的第一人。2002年8月，在北京召開的國際數學家大會，標志著中國數學進入嶄新的時代，大會會徽就是這個“弦圖”，寓意中國古代數學取得的重要成果。

證法二：

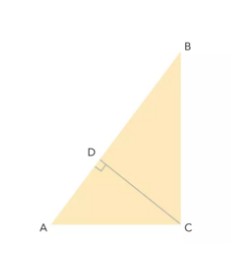
證法三：

這一證法涉及到圓內相交弦定理：m·n＝p·q（如左圖），再看AB和CD垂直的情況，相交弦定理仍然成立（如右圖），因此(c－a)(c＋a)＝b2。即得c2－a2＝b2于是，a2＋b2＝c2。

勾股定理的公式

勾股定理，公式表達為：a2+b2=c2，其中a、b分別為直角邊，c直角三角形的斜邊。譬如a=3，b=4，那么得c=5。這個三角形的面積S=ab/2=3×4/2=6。

勾股定理是一個基本的幾何定理，指直角三角形的兩條直角邊的平方和等于斜邊的平方。中國古代稱直角三角形為勾股形，并且直角邊中較小者為勾，另一長直角邊為股，斜邊為弦，所以稱這個定理為勾股定理，也有人稱商高定理。