方程無(wú)解是在一定的范圍內(nèi)沒(méi)有任何的數(shù)滿(mǎn)足該方程,求方程的解的過(guò)程叫解方程。如方程組x+y=4①2x+2y=10②,因?yàn)榉匠挞诨?jiǎn)后為x+y=5,這與方程①相矛盾,所以此類(lèi)方程組無(wú)解。

方程無(wú)解
無(wú)解的意思是在一定的范圍內(nèi)沒(méi)有任何的數(shù)滿(mǎn)足該方程。求方程的解的過(guò)程叫解方程。注意:解方程有時(shí)找不到它的解,稱(chēng)方程無(wú)解,確定方程無(wú)解的過(guò)程也叫解方程。
實(shí)例
無(wú)解不是無(wú)實(shí)根(無(wú)實(shí)解),認(rèn)識(shí)的數(shù)理范圍是復(fù)數(shù)(包含了實(shí)數(shù)與虛數(shù)兩大部分)比如X^2=-1。
這在實(shí)數(shù)范圍沒(méi)有解(無(wú)實(shí)解)但絕不能說(shuō)無(wú)解。在虛數(shù)或者更大范圍的復(fù)數(shù)圈里,就有解X=i其中i是虛數(shù)單位。
最典型的沒(méi)有解的方程是1/x=0在復(fù)數(shù)范圍仍然沒(méi)有解。也許有人會(huì)說(shuō)解是x=∞。實(shí)際上“∞”只是符號(hào)不是“數(shù)”,自然不能作為解了。
分式方程無(wú)解
分式方程無(wú)解則是指不論未知數(shù)取何值,都不能使方程兩邊的值相等。它包含兩種情形:其一,原方程化去分母后的整式方程無(wú)解;其二,原方程化去分母后的整式方程有解,但這個(gè)解卻使原方程的分母為0,它是原方程的增根,從而使原方程無(wú)解。

方程是指含有未知數(shù)的等式。是表示兩個(gè)數(shù)學(xué)式之間相等關(guān)系的一種等式,使等式成立的未知數(shù)的值稱(chēng)為“解”或“根”。求方程的解的過(guò)程稱(chēng)為“解方程”。...

對(duì)的。方程是指含有未知數(shù)的等式,是表示兩個(gè)數(shù)學(xué)式之間相等關(guān)系的一種等式,使等式成立的未知數(shù)的值稱(chēng)為“解”或“根”。求方程的解的過(guò)程稱(chēng)為“解方...

使方程兩邊相等的未知數(shù)的值叫做方程的解,只含一個(gè)未知數(shù)的方程的解,也叫方程的根。方程的根可以叫方程的解,但方程的解不一定可以叫方程的根。方程...
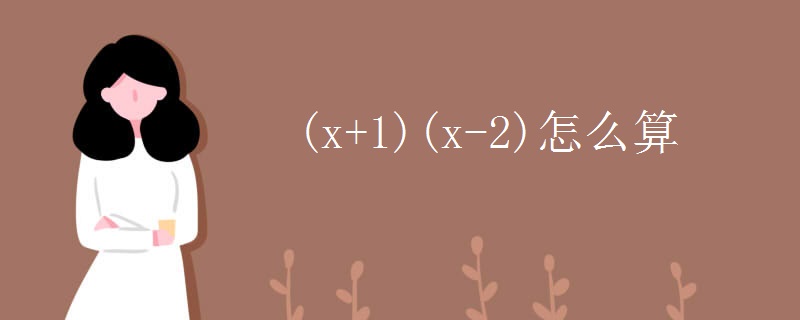
解:(x+1)(x-2)=x2-2x+x-2=x2-x-2。故答案為x2-x-2。方程是指含有未知數(shù)的等式。是表示兩個(gè)數(shù)學(xué)式(如兩個(gè)數(shù)、函數(shù)...

方程是指含有未知數(shù)的等式。是表示兩個(gè)數(shù)學(xué)式,如兩個(gè)數(shù)、函數(shù)、量、運(yùn)算之間相等關(guān)系的一種等式,使等式成立的未知數(shù)的值稱(chēng)為“解”或“根”;含有等...

方程是指含有未知數(shù)的等式。是表示兩個(gè)數(shù)學(xué)式(如兩個(gè)數(shù)、函數(shù)、量、運(yùn)算)之間相等關(guān)系的一種等式,使等式成立的未知數(shù)的值稱(chēng)為“解”或“根”。在數(shù)...

1、有分母先去分母。2、有括號(hào)就去括號(hào)。3、需要移項(xiàng)就進(jìn)行移項(xiàng)。4、合并同類(lèi)項(xiàng)。5、系數(shù)化為1求得未知數(shù)的值。6、開(kāi)頭要寫(xiě)“解”。

對(duì)一些簡(jiǎn)單的三次方程能用因式分解求解,用因式分解法求解很方便,直接把三次方程降次。例如:解方程x^3-x=0,對(duì)左邊作因式分解,得x(x+1...