各位同學在查看時請點擊全屏查看

2017年伊春中考數(shù)學試題

一、數(shù)學試題填空題（每題3分，滿分30分）

1．“可燃冰”的開發(fā)成功，拉開了我國開發(fā)新能源的大門，目前發(fā)現(xiàn)我國南海“可燃冰”儲存量達到800億噸，將800億噸用科學記數(shù)法可表示為　? 　噸．

【答案】8×1010

2．在函數(shù)y= 中，自變量x的取值范圍是　　．

【答案】x≠1

3．如圖，BC∥EF，AC∥DF，添加一個條件　　，使得△ABC≌△DEF．

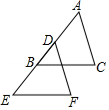
【答案】AB=DE或BC=EF或AC=DF

4．在一個不透明的袋子中裝有除顏色外完全相同的3個白球、若干紅球，從中隨機摸取1個球，摸到紅球的概率是 ，則這個袋子中有紅球　　個．

【答案】5

5．若關(guān)于x的一元一次不等式組 無解，則a的取值范圍是　　．

【答案】a≥2

6．為了鼓勵居民節(jié)約用水，某自來水公司采取分段計費，每月每戶用水不超過10噸，每噸2.2元；超過10噸的部分，每噸加收1.3元．小明家4月份用水15噸，應(yīng)交水費　　元．

【答案】39.5

7．如圖，BD是⊙O的切線，B為切點，連接DO與⊙O交于點C，AB為⊙O的直徑，連接CA，若∠D=30°，⊙O的半徑為4，則圖中陰影部分的面積為　??????? ．

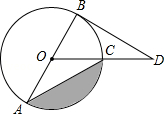
【答案】π-4? 　

8．圓錐的底面半徑為2cm，圓錐高為3cm，則此圓錐側(cè)面展開圖的周長為　?? 　cm．

【答案】（2 +4π）

9．如圖，在△ABC中，AB=BC=8，AO=BO，點M是射線CO上的一個動點，∠AOC=60°，則當△ABM為直角三角形時，AM的長為　　．

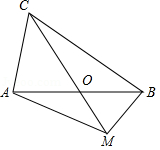
【答案】4或4或4

10．如圖，四條直線l1：y1=x，l2：y2=x，l3：y3=﹣x，l4：y4=﹣x，OA1=1，過點A1作A1A2⊥x軸，交l1于點A2，再過點A1作A1A2⊥l1交l2于點A2，再過點A2作A2A3⊥l3交y軸于點A3…，則點A2017坐標為　??? 　．

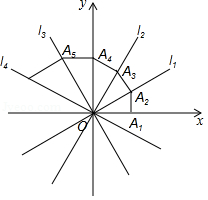
【答案】[（）2015，（）2016]

二、選擇題（每題3分，滿分30分）

11．下列運算中，計算正確的是（　　）

A．（a2b）3=a5b3????????????? B．（3a2）3=27a6????????????? C．x6÷x2=x3????????????? D．（a+b）2=a2+b2

【答案】B

12．下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（　　）

A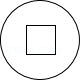．????????????? B．????????????? C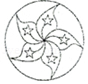．????????????? D．

【答案】A

13．如圖，是由若干個相同的小立方體搭成的幾何體體俯視圖和左視圖．則小立方體的個數(shù)可能是（　　）

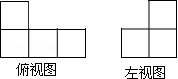
A．5或6????????????? B．5或7????????????? C．4或5或6????????????? D．5或6或7

【答案】D

14．某市4月份日平均氣溫統(tǒng)計圖情況如圖所示，則在日平均氣溫這組數(shù)據(jù)中，眾數(shù)和中位數(shù)分別是（　　）

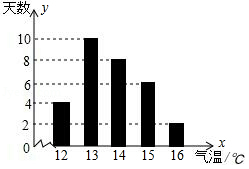
A．13，13????????????? B．13，13.5????????????? C．13，14????????????? D．16，13

【答案】C

15．如圖，某工廠有甲、乙兩個大小相同的蓄水池，且中間有管道連通，現(xiàn)要向甲池中注水，若單位時間內(nèi)的注水量不變，那么從注水開始，乙水池水面上升的高度h與注水時間t之間的函數(shù)關(guān)系圖象可能是（　　）

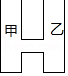
A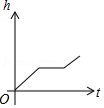．????????????? B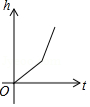．????????????? C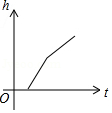．????????????? D．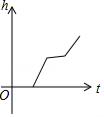

【答案】D

16．反比例函數(shù)y= 圖象上三個點的坐標為（x1，y1）、（x2，y2）、（x3，y3），若x1＜x2＜0＜x3，則y1，y2，y3的大小關(guān)系是 （　　）

A．y1＜y2＜y3????????????? B．y2＜y1＜y3????????????? C．y2＜y3＜y1????????????? D．y1＜y3＜y2

【答案】B

17．已知關(guān)于x的分式方程解是非負數(shù)，那么a的取值范圍是（　　）

A．a(chǎn)＞1????????????? B．a(chǎn)≥1????????????? C．a(chǎn)≥1且a≠9????????????? D．a(chǎn)≤1

【答案】C

18．如圖，在矩形ABCD中，AD=4，∠DAC=30°，點P、E分別在AC、AD上，則PE+PD的最小值是（　　）

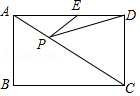
A．2????????????? B．2 ????????????? C．4????????????? D．

【答案】B

19． “雙11”促銷活動中，小芳的媽媽計劃用1000元在唯品會購買價格分別為80元和120元的兩種商品，則可供小芳媽媽選擇的購買方案有（　　）

A．4種????????????? B．5種????????????? C．6種????????????? D．7種

【答案】A

20．如圖，在邊長為4的正方形ABCD中，E、F是AD邊上的兩個動點，且AE=FD，連接BE、CF、BD，CF與BD交于點G，連接AG交BE于點H，連接DH，下列結(jié)論正確的個數(shù)是（　　）

①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG：S△HBG=tan∠DAG ⑤線段DH的最小值是2﹣2．

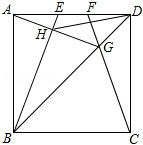
A．2????????????? B．3????????????? C．4????????????? D．5

【答案】C

三、解答題（滿分60分）

21．先化簡，再求值： ，其中a=1+2cos60°．

= = =，

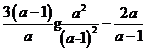當a=1+2cos60°=1+2×=1+1=2時，原式= =2．

22．如圖，在平面直角坐標系中，△ABC的三個頂點都在格點上，點A的坐標為（2，2）請解答下列問題：

（1）畫出△ABC關(guān)于y軸對稱的△A1B1C1，并寫出A1的坐標．

（2）畫出△ABC繞點B逆時針旋轉(zhuǎn)90°后得到的△A2B2C2，并寫出A2的坐標．

（3）畫出△A2B2C2關(guān)于原點O成中心對稱的△A3B3C3，并寫出A3的坐標．

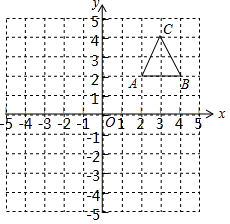
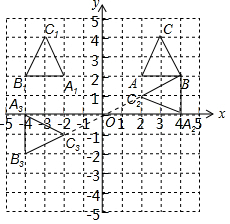
（1）畫出△ABC關(guān)于y軸對稱的△A1B1C1，如圖所示，此時A1的坐標為（﹣2，2）；

（2）畫出△ABC繞點B逆時針旋轉(zhuǎn)90°后得到的△A2B2C2，如圖所示，此時A2的坐標為（4，0）；

（3）畫出△A2B2C2關(guān)于原點O成中心對稱的△A3B3C3，如圖所示，此時A3的坐標為（﹣4，0）．

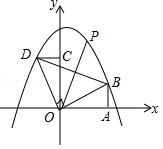
23．如圖，Rt△AOB的直角邊OA在x軸上，OA=2，AB=1，將Rt△AOB繞點O逆時針旋轉(zhuǎn)90°得到Rt△COD，拋物線y=﹣x2+bx+c經(jīng)過B、D兩點．

（1）求二次函數(shù)的解析式；

（2）連接BD，點P是拋物線上一點，直線OP把△BOD的周長分成相等的兩部分，求點P的坐標．

（1）由旋轉(zhuǎn)性質(zhì)可得CD=AB=1、OA=OC=2，從而得出點B、D坐標，代入解析式即可得出答案；

（2）由直線OP把△BOD的周長分成相等的兩部分且OB=OD，知DQ=BQ，即點Q為BD的中點，從而得出點Q坐標，求得直線OP解析式，代入拋物線解析式可得點P坐標．

試題解析：（1）∵Rt△AOB繞點O逆時針旋轉(zhuǎn)90°得到Rt△COD，

∴CD=AB=1、OA=OC=2，

則點B（2，1）、D（﹣1，2），代入解析式，得： ，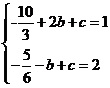

解得： ，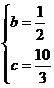

∴二次函數(shù)的解析式為y=﹣ x2+x+；

（2）如圖，

∵直線OP把△BOD的周長分成相等的兩部分，且OB=OD，

∴DQ=BQ，即點Q為BD的中點，

∴點Q坐標為（，），

設(shè)直線OP解析式為y=kx，

將點Q坐標代入，得：k=，

解得：k=3，

∴直線OP的解析式為y=3x，

代入y=﹣ x2+x+，得：y=﹣ x2+x+=3x，

解得：x=1或x=﹣4（舍），

當x=1時，y=3，

∴點P坐標為（1，3）．

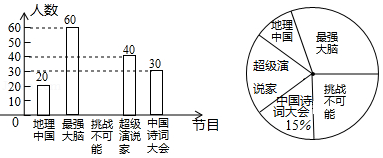
24．我市某中學為了了解孩子們對《中國詩詞大會》，《挑戰(zhàn)不可能》，《最強大腦》，《超級演說家》，《地理中國》五種電視節(jié)目的喜愛程度，隨機在七、八、九年級抽取了部分學生進行調(diào)查（每人只能選擇一種喜愛的電視節(jié)目），并將獲得的數(shù)據(jù)進行整理，繪制出以下兩幅不完整的統(tǒng)計圖，請根據(jù)兩幅統(tǒng)計圖中的信息回答下列問題：

（1）本次調(diào)查中共抽取了　　名學生．

（2）補全條形統(tǒng)計圖．

（3）在扇形統(tǒng)計圖中，喜愛《地理中國》節(jié)目的人數(shù)所在的扇形的圓心角是　　度．

（4）若該學校有2000人，請你估計該學校喜歡《最強大腦》節(jié)目的學生人數(shù)是多少人？

．

（1）根據(jù)題意列式計算即可；

（2）求得喜愛《挑戰(zhàn)不可能》節(jié)目的人數(shù)，將條形統(tǒng)計圖補充完整即可；

（3）用360°×喜愛《地理中國》節(jié)目的人數(shù)占總?cè)藬?shù)的百分數(shù)即可得到結(jié)論；

（4）直接利用樣本估計總體的方法求解即可求得答案．

試題解析：（1）30÷15%=200名，

答：本次調(diào)查中共抽取了200名學生；

故答案為：200；

（2）喜愛《挑戰(zhàn)不可能》節(jié)目的人數(shù)=200﹣20﹣60﹣40﹣30=50名，

補全條形統(tǒng)計圖如圖所示；

（3）喜愛《地理中國》節(jié)目的人數(shù)所在的扇形的圓心角是360°× =36°；

故答案為：36；

（4）2000× =600名，

答：該學校喜歡《最強大腦》節(jié)目的學生人數(shù)是600人．

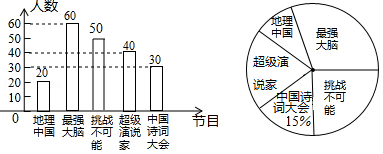
25．在甲、乙兩城市之間有一服務(wù)區(qū)，一輛客車從甲地駛往乙地，一輛貨車從乙地駛往甲地．兩車同時出發(fā)，勻速行駛，客車、貨車離服務(wù)區(qū)的距離y1（千米），y2（千米）與行駛的時間x（小時）的函數(shù)關(guān)系圖象如圖1所示．

（1）甲、乙兩地相距　? 千米．

（2）求出發(fā)3小時后，貨車離服務(wù)區(qū)的路程y2（千米）與行駛時間x（小時）之間的函數(shù)關(guān)系式．

（3）在客車和貨車出發(fā)的同時，有一輛郵政車從服務(wù)區(qū)勻速去甲地取貨后返回乙地（取貨的時間忽略不計），郵政車離服務(wù)區(qū)的距離y3（千米）與行駛時間x（小時）之間的函數(shù)關(guān)系圖線如圖2中的虛線所示，直接寫出在行駛的過程中，經(jīng)過多長時間郵政車與客車和貨車的距離相等？

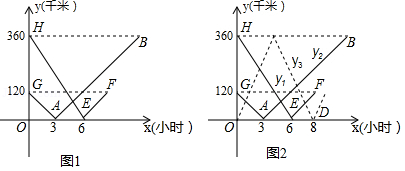
（1）根據(jù)圖1，根據(jù)客車、貨車離服務(wù)區(qū)的初始距離可得甲乙兩地距離；

（2）根據(jù)圖象中的數(shù)據(jù)可以求得3小時后，貨車離服務(wù)區(qū)的路程y2與行駛時間x之間的函數(shù)關(guān)系式；

（3）分兩種情況討論，當郵政車去甲地的途中會有某個時間郵政車與客車和貨車的距離相等；當郵政車從甲地返回乙地時，貨車與客車相遇時，郵政車與客車和貨車的距離相等．

試題解析：（1）360+120=480（千米）

故答案為：480；

（2）設(shè)3小時后，貨車離服務(wù)區(qū)的路程y2與行駛時間x之間的函數(shù)關(guān)系式為y2=kx+b，

由圖象可得，貨車的速度為：120÷3=40千米/時，

則點B的橫坐標為：3+360÷40=12，

∴點P的坐標為（12，360），

則有 ，解得 ，

即3小時后，貨車離服務(wù)區(qū)的路程y2與行駛時間x之間的函數(shù)關(guān)系式為y2=40x﹣120；

（3）v客=360÷6=60千米/時，

v郵=360×2÷8=90千米/時，

設(shè)當郵政車去甲地的途中時，經(jīng)過t小時郵政車與客車和貨車的距離相等，

120+（90﹣40）t=360﹣（60+90）t

t=1.2（小時）；

設(shè)當郵政車從甲地返回乙地時，經(jīng)過t小時郵政車與客車和貨車的距離相等，

40t+60t=480

解得t=4.8，

綜上所述，經(jīng)過1.2或4.8小時郵政車與客車和貨車的距離相等．

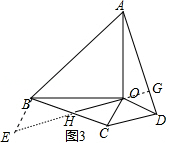
26．已知：△AOB和△COD均為等腰直角三角形，∠AOB=∠COD=90°．連接AD，BC，點H為BC中點，連接OH．

（1）如圖1所示，易證：OH= AD且OH⊥AD（不需證明）

（2）將△COD繞點O旋轉(zhuǎn)到圖2，圖3所示位置時，線段OH與AD又有怎樣的關(guān)系，并選擇一個圖形證明你的結(jié)論．

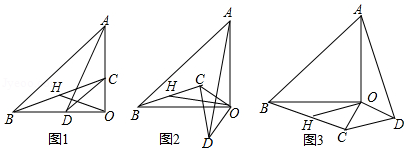
（1）只要證明△AOD≌△BOC，即可解決問題；

（2）①如圖2中，結(jié)論：OH=AD，OH⊥AD．延長OH到E，使得HE=OH，連接BE，由△BEO≌△ODA即可解決問題；

②如圖3中，結(jié)論不變．延長OH到E，使得HE=OH，連接BE，延長EO交AD于G．由△BEO≌△ODA即可解決問題；

試題解析：（1）如圖1中，

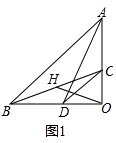
∵△OAB與△OCD為等腰直角三角形，∠AOB=∠COD=90°，

∴OC=OD，OA=OB，

∵在△AOD與△BOC中， ，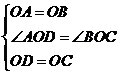

∴△AOD≌△BOC（SAS），

∴∠ADO=∠BCO，∠OAD=∠OBC，

∵點H為線段BC的中點，

∴OH=HB，

∴∠OBH=∠HOB=∠OAD，

又因為∠OAD+∠ADO=90°，

所以∠ADO+∠BOH=90°，

所以O(shè)H⊥AD

（2）①結(jié)論：OH=AD，OH⊥AD，如圖2中，延長OH到E，使得HE=OH，連接BE，

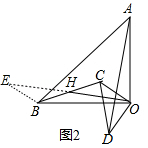
易證△BEO≌△ODA

∴OE=AD

∴OH=OE=AD

由△BEO≌△ODA，知∠EOB=∠DAO

∴∠DAO+∠AOH=∠EOB+∠AOH=90°，

∴OH⊥AD．

②如圖3中，結(jié)論不變．延長OH到E，使得HE=OH，連接BE，延長EO交AD于G．

易證△BEO≌△ODA

∴OE=AD

∴OH=OE=AD

由△BEO≌△ODA，知∠EOB=∠DAO

∴∠DAO+∠AOF=∠EOB+∠AOG=90°，

∴∠AGO=90°

∴OH⊥AD．

27．為了推動“龍江經(jīng)濟帶”建設(shè)，我省某蔬菜企業(yè)決定通過加大種植面積、增加種植種類，促進經(jīng)濟發(fā)展．2017年春，預(yù)計種植西紅柿、馬鈴薯、青椒共100公頃（三種蔬菜的種植面積均為整數(shù)），青椒的種植面積是西紅柿種植面積的2倍，經(jīng)預(yù)算，種植西紅柿的利潤可達1萬元/公頃，青椒1.5萬元/公頃，馬鈴薯2萬元/公頃，設(shè)種植西紅柿x公頃，總利潤為y萬元．

（1）求總利潤y（萬元）與種植西紅柿的面積x（公頃）之間的關(guān)系式．

（2）若預(yù)計總利潤不低于180萬元，西紅柿的種植面積不低于8公頃，有多少種種植方案？

（3）在（2）的前提下，該企業(yè)決定投資不超過獲得最大利潤的在冬季同時建造A、B兩種類型的溫室大棚，開辟新的經(jīng)濟增長點，經(jīng)測算，投資A種類型的大棚5萬元/個，B種類型的大棚8萬元/個，請直接寫出有哪幾種建造方案？

（1）根據(jù)總利潤=三種蔬菜的利潤之和，計算即可；

（2）由題意，列出不等式組即可解決問題；

（3）由題意，列出二元一次不等式，求出整數(shù)解即可；

試題解析：（1）由題意y=x+1.5×2x+2（100﹣3x）=﹣2x+200．

（2）由題意﹣2x+200≥180，

解得x≤10，

∵x≥8，

∴8≤x≤10．

∵x為整數(shù)，

∴x=8，9，10．

∴有3種種植方案，

方案一：種植西紅柿8公頃、馬鈴薯76公頃、青椒16公頃．

方案二：種植西紅柿9公頃、馬鈴薯73公頃、青椒18公頃．

方案三：種植西紅柿10公頃、馬鈴薯70公頃、青椒20公頃．

（3）∵y=﹣2x+200，

﹣2＜0，

∴x=8時，利潤最大，最大利潤為184萬元．

設(shè)投資A種類型的大棚a個，B種類型的大棚b個，

由題意5a+8b≤×184，

∴5a+8b≤23，

∴a=1，b=1或2，

a=2，b=1，

a=3，b=1，

∴可以投資A種類型的大棚1個，B種類型的大棚1個，

或投資A種類型的大棚1個，B種類型的大棚2個，

或投資A種類型的大棚2個，B種類型的大棚1個，

或投資A種類型的大棚3個，B種類型的大棚1個．

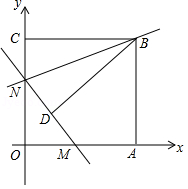
28．如圖，矩形AOCB的頂點A、C分別位于x軸和y軸的正半軸上，線段OA、OC的長度滿足方程|x﹣15|+ =0（OA＞OC），直線y=kx+b分別與x軸、y軸交于M、N兩點，將△BCN沿直線BN折疊，點C恰好落在直線MN上的點D處，且tan∠CBD=

（1）求點B的坐標；

（2）求直線BN的解析式；

（3）將直線BN以每秒1個單位長度的速度沿y軸向下平移，求直線BN掃過矩形AOCB的面積S關(guān)于運動的時間t（0＜t≤13）的函數(shù)關(guān)系式．

（1）由非負數(shù)的性質(zhì)可求得x、y的值，則可求得B點坐標；

（2）過D作EF⊥OA于點E，交CB于點F，由條件可求得D點坐標，且可求得 ,結(jié)合DE∥ON，利用平行線分線段成比例可求得OM和ON的長，則可求得N點坐標，利用待定系數(shù)法可求得直線BN的解析式；

（3）設(shè)直線BN平移后交y軸于點N′，交AB于點B′，當點N′在x軸上方時，可知S即為?BNN′B′的面積，當N′在y軸的負半軸上時，可用t表示出直線B′N′的解析式，設(shè)交x軸于點G，可用t表示出G點坐標，由S=S四邊形BNN′B′﹣S△OGN′，可分別得到S與t的函數(shù)關(guān)系式．

試題解析：（1）∵|x﹣15|+=0，

∴x=15，y=13，

∴OA=BC=15，AB=OC=13，

∴B（15，13）；

（2）如圖1，過D作EF⊥OA于點E，交CB于點F，

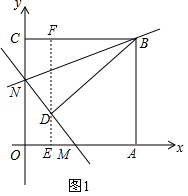
由折疊的性質(zhì)可知BD=BC=15，∠BDN=∠BCN=90°，

∵tan∠CBD=，

∴,且BF2+DF2=BD2=152，解得BF=12，DF=9，

∴CF=OE=15﹣12=3，DE=EF﹣DF=13﹣9=4，

∵∠CND+∠CBD=360°﹣90°﹣90°=180°，且∠ONM+∠CND=180°，

∴∠ONM=∠CBD，

∴,

∵DE∥ON，

∴,且OE=3，

∴,解得OM=6，

∴ON=8，即N（0，8），

把N、B的坐標代入y=kx+b可得 ，解得 ，

∴直線BN的解析式為y= x+8；

（3）設(shè)直線BN平移后交y軸于點N′，交AB于點B′，

當點N′在x軸上方，即0＜t≤8時，如圖2，

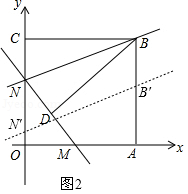
由題意可知四邊形BNN′B′為平行四邊形，且NN′=t，

∴S=NN′?OA=15t；

當點N′在y軸負半軸上，即8＜t≤13時，設(shè)直線B′N′交x軸于點G，如圖3，

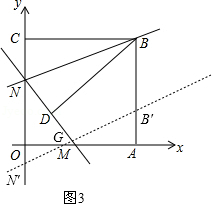
∵NN′=t，

∴可設(shè)直線B′N′解析式為y=x+8﹣t，

令y=0，可得x=3t﹣24，

∴OG=24，

∵ON=8，NN′=t，

∴ON′=t﹣8，

∴S=S四邊形BNN′B′﹣S△OGN′=15t﹣（t﹣8）（3t﹣24）=﹣t2+39t﹣96；

綜上可知S與t的函數(shù)關(guān)系式為S=