各位同學在查看時請點擊全屏查看

2016年晉中中考數(shù)學試題

一、數(shù)學試題選擇題（本大題共10小題，每小題3分，共30分．在每個小題給出的四個選項中，只有一項符合題目要求，請選出并在答題卡上將該項涂黑）

1．的相反數(shù)是（）

A．? B．-6C．6? D．

2．不等式組的解集是（ ）

A．x>5B．x<3 C．-5<x<3 D．x<5

3．以下問題不適合全面調(diào)查的是（）

A．調(diào)查某班學生每周課前預習的時間B．調(diào)查某中學在職教師的身體健康狀況

C．調(diào)查全國中小學生課外閱讀情況? D．調(diào)查某籃球隊員的身高

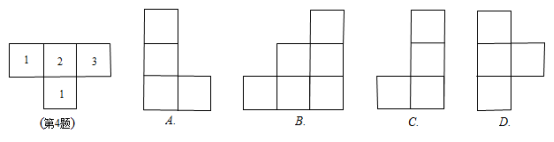
4．如圖是由幾個大小相同的小正方體搭成的幾何體的俯視圖，小正方體中的數(shù)字表示該位置小正方體的個數(shù)，則該幾何體的左視圖是（ ）

5．（2016·山西）我國計劃在2020年左右發(fā)射火星探測衛(wèi)星．據(jù)科學研究，火星距離地球的最近距離約為5500萬千米，這個數(shù)據(jù)用科學計數(shù)法可表示為（）

A． B．C．D．

6．下列運算正確的是 （）

A． B．C．? D．

7．甲、乙兩個搬運工搬運某種貨物，已知乙比甲每小時多搬運600kg，甲搬運5000kg所用的時間與乙搬運8000kg所用的時間相等，求甲、乙兩人每小時分別搬運多少kg貨物．設甲每小時搬運xkg貨物，則可列方程為（）

A．? B．?

C．? D．

8．將拋物線向左平移3個單位，再向上平移5個單位，得到拋物線的表達式為（）

A．? B．C．D．

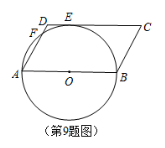
9．如圖，在ABCD中，AB為的直徑，與DC相切于點E，與AD相交于點F，已知AB=12，，則的長為（）

A．? B． C．? D．

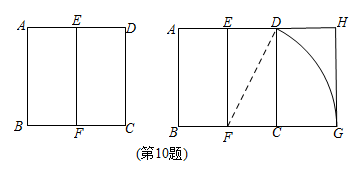
10．寬與長的比是（約為0．618）的矩形叫做黃金矩形．黃金矩形蘊藏著豐富的美學價值，給我們以協(xié)調(diào)和勻稱的美感．我們可以用這樣的方法畫出黃金矩形：作正方形ABCD，分別取AD，BC的中點E，F(xiàn)，連接EF；以點F為圓心，以FD為半徑畫弧，交BC的延長線與點G；作，交AD的延長線于點H．則圖中下列矩形是黃金矩形的是（）

A．矩形ABFE? B．矩形EFCD C．矩形EFGHD．矩形DCGH

二、填空題（本大題共5個小題，每小題3分，共15分）

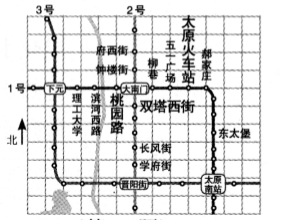
11．如圖是利用網(wǎng)格畫出的太原市地鐵1，2，3號線路部分規(guī)劃示意圖．若建立適當?shù)钠矫嬷苯亲鴺讼担硎倦p塔西街點的坐標為（0，-1），表示桃園路的點的坐標為（-1，0），則表示太原火車站的點（正好在網(wǎng)格點上）的坐標是．

12．已知點（m-1，），（m-3，）是反比例函數(shù)圖象上的兩點，則（填“>”或“=”或“<”）

13．如圖是一組有規(guī)律的圖案，它們是由邊長相同的小正方形組成，其中部分小正方形涂有陰影，依此規(guī)律，第n個圖案中有個涂有陰影的小正方形（用含有n的代數(shù)式表示）．

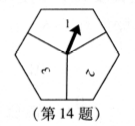
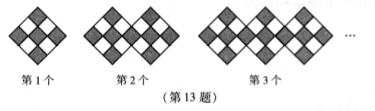
14．如圖是一個能自由轉動的正六邊形轉盤，這個轉盤被三條分割線分成形狀相同，面積相等的三部分，且分別標有“1”“2”“3”三個數(shù)字，指針的位置固定不動．讓轉盤自動轉動兩次，當指針指向的數(shù)都是奇數(shù)的概率為

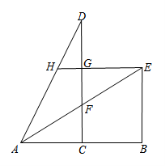
15．如圖，已知點C為線段AB的中點，CD⊥AB且CD=AB=4，連接AD，BE⊥AB，AE是的平分線，與DC相交于點F，EH⊥DC于點G，交AD于點H，則HG的長為

三、解答題（本大題共8個小題，共75分．解答應寫出文字說明、證明過程或演算步驟）

16．（本題共2個小題，每小題5分，共10分）

（1）計算：

（2）先化簡，在求值：，其中x=-2．

17．（本題7分）解方程：

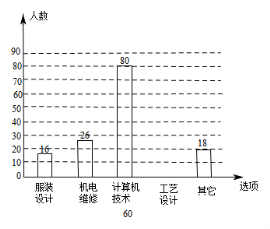18．（本題8分）每年5月的第二周為：“職業(yè)教育活動周”，今年我省展開了以“弘揚工匠精神，打造技能強國”為主題的系列活動，活動期間某職業(yè)中學組織全校師生并邀請學生家長和社區(qū)居民參加“職教體驗觀摩”活動，相關職業(yè)技術人員進行了現(xiàn)場演示，活動后該校隨機抽取了部分學生進行調(diào)查：“你最感興趣的一種職業(yè)技能是什么？”并對此進行了統(tǒng)計，繪制了統(tǒng)計圖（均不完整）．

（1）補全條形統(tǒng)計圖和

扇形統(tǒng)計圖；

（2）若該校共有1800名學生，請估計該校對“工業(yè)設計”最感興趣的學生有多少人?

（3）要從這些被調(diào)查的 學生中隨機抽取一人進 行訪談，那么正好抽到對“機電維修”最

? 感興趣的學生的概率是?

19．（本題7分）請閱讀下列材料，并完成相應的任務：

阿基米德折弦定理

? 阿基米德（Archimedes，公元前287~公元212年，古希臘）是有史以來最偉大的數(shù)學家之一．他與牛頓、高斯并稱為三大數(shù)學王子．

阿拉伯Al-Biruni（973年~1050年）的譯文中保存了阿基米德折弦定理的內(nèi)容，蘇聯(lián)在1964年根據(jù)Al-Biruni譯本出版了俄文版《阿基米德全集》，第一題就是阿基米德的折弦定理．

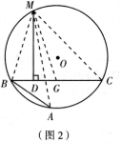
阿基米德折弦定理：如圖1，AB和BC是的兩條弦（即折線ABC是圓的一條折弦），BC>AB，M是的中點，則從M向BC所作垂線的垂足D是折弦ABC的中點，即CD=AB+BD．

下面是運用“截長法”證明CD=AB+BD的部分證明過程．

證明：如圖2，在CB上截取CG=AB，連接MA，MB，MC和MG．

∵M是的中點，[來源:學科網(wǎng)]

∴MA=MC

? ．．．

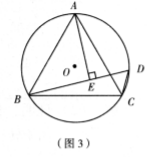
任務：（1）請按照上面的證明思路，寫出該證明的剩余部分；[來源:.Com]

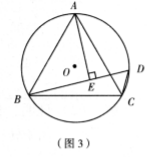
（2）填空：如圖（3），已知等邊△ABC內(nèi)接于，AB=2，D為

? 上 一點, ，AE⊥BD與點E，則△BDC的長是 ．

20．（本題7分）我省某蘋果基地銷售優(yōu)質(zhì)蘋果，該基地對需要送貨

且購買量在2000kg~5000kg（含2000kg和5000kg）的客戶有兩種

銷售方案（客戶只能選擇其中一種方案）：

方案A：每千克5．8元，由基地免費送貨．

方案B：每千克5元，客戶需支付運費2000元．

（1）請分別寫出按方案A，方案B購買這種蘋果的應付款y（元）與購買量x（kg）之間的函數(shù)表達式；

（2）求購買量x在什么范圍時，選用方案A比方案B付款少；

（3）某水果批發(fā)商計劃用20000元，選用這兩種方案中的一種，購買盡可能多的這種蘋果，請直接寫出他應選擇哪種方案．

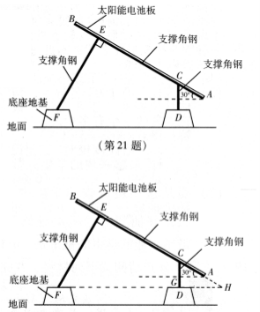
21．（本題10分）太陽能光伏發(fā)電因其清潔、安全、便利、高效等特點，已成為世界各國普遍關注和重點發(fā)展的新興產(chǎn)業(yè)，如圖是太陽能電池板支撐架的截面圖，其中的粗線表示支撐角鋼，太陽能電池板與支撐角鋼AB的長度相同，均為300cm，AB的傾斜角為，BE=CA=50cm，支撐角鋼CD，EF與底座地基臺面接觸點分別為D，F(xiàn)，CD垂直于地面，于點E．兩個底座地基高度相同（即點D，F(xiàn)到地面的垂直距離相同），均為30cm，點A到地面的垂直距離為50cm，求支撐角鋼CD和EF的長度各是多少cm（結果保留根號）

22．（本題12分）綜合與實踐[來源:學§科§網(wǎng)Z§X§X§K]

問題情境

在綜合與實踐課上，老師讓同學們以“菱形紙片的剪拼”為主題開展數(shù)學活動，如圖1，將一張菱形紙片ABCD（）沿對角線AC剪開，得到和．

操作發(fā)現(xiàn)

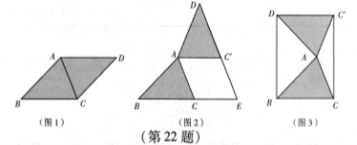（1）將圖1中的以A為旋轉中心，

? 逆時針方向旋轉角，使? ，

? 得到如圖2所示的，分別延長BC?

? 和交于點E，則四邊形的

狀是? ；……………（2分）

（2）創(chuàng)新小組將圖1中的以A為

旋轉中心，按逆時針方向旋轉角

，使，得到如圖3所

示的，連接DB，，得到四邊形，發(fā)現(xiàn)它是矩形．請你證明這個論；

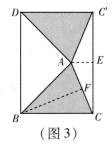
實踐探究

（3）縝密小組在創(chuàng)新小組發(fā)現(xiàn)結論的基礎上，量得圖3中BC=13cm，AC=10cm，然后提出一個問題：將沿著射線DB方向平移acm，得到，連接，，使四邊形恰好為正方形，求a的值．請你解答此問題；

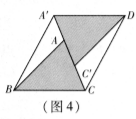（4）請你參照以上操作，將圖1中的在同一平面內(nèi)進行一次平移，得到，在圖4中畫出平移后構造出的新圖形，標明字母，說明平移及構圖方法，寫出你發(fā)現(xiàn)的結論，不必證明．

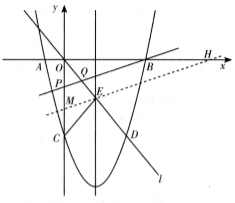
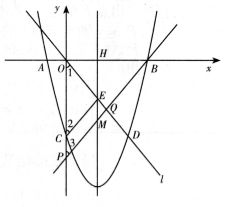
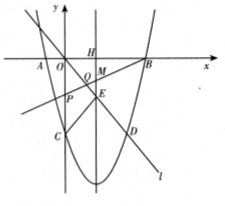
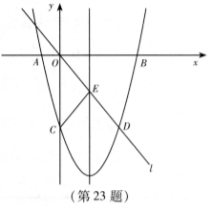23.如圖，在平面直角坐標系中，已知拋物線與x軸交于A，B兩點，與y軸交于點C，直線l經(jīng)過坐標原點O，與拋物線的一個交點為D，與拋物線的對稱軸交于點E，連接CE，已知點A，D的坐標分別為（－2，0），（6，－8）．

（1）          求拋物線的函數(shù)表達式，并分別求出點B和點E的坐標；

（2）          試探究拋物線上是否存在點F，使≌，若存在，請直接寫出點F的坐標；若不存在，請說明理由；

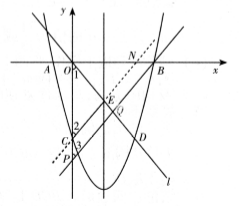
（3）          若點P是y軸負半軸上的一個動點，設其坐標為（0，m），直線PB與直線l交于點Q．試探究：當m為何值時，是等腰三角形．

2016年晉中中考數(shù)學試題參考答案

一、選擇題（本大題共10小題，每小題3分，共30分．在每個小題給出的四個選項中，只有一項符合題目要求，請選出并在答題卡上將該項涂黑）

1． A　　 2． C? 　3．C? 　　4． A 　　5．B 　　

6．D 　　7．B 　　8．D 　　　9．C 　　　10．D

二、填空題（本大題共5個小題，每小題3分，共15分）

11． （3，0） ．

12． >?

13．（4n+1）

14．

15．

16．（1）解答：原=9-5-4+1? ……………………………（4分）

=1．……………………………（5分）

（2）解答：原式=? ……………………………（2分）

=? ……………………………（3分）

= ……………………………（4分）

當x=-2時，原式=? ……………………（5分）

17．? 解答：解法一：

? 原方程可化為? ……………………………（1分）

? ．……………………………（2分）

? ．? ……………………………（3分）

? ．……………………………（4分）

? ∴? x-3=0或x-9=0．? ……………………………（5分）

? ∴ ，． ……………………………（7分）

? 解法二：

? 原方程可化為

……………………………（3分）

這里a=1，b=-12，c=27．∵

? ∴． ……………………………（5分）

因此原方程的根為 ，． ……………………………（7分）

18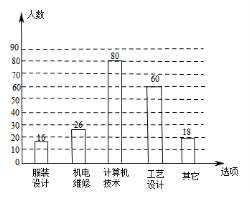．解答：（1）補全的扇形統(tǒng)計圖和條形統(tǒng)計圖如圖所示

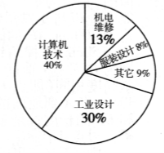
（2）1800×30%=540（人）

∴估計該校對“工業(yè)設計”最感興趣的學生是540人

? （3）要從這些被調(diào)查的學生中隨機抽取一人進行訪談，那么正好抽到對“機電維修”

最感興趣的學生的概率是 0.13（或13%或）

19． 解答：（1）證明：又∵，? …………………（1分）

∴ △MBA≌△MGC．…………………（2分）

∴MB=MG．? …………………（3分）

又∵MD⊥BC，∵BD=GD． …………………（4分）

∴CD=CG+GD=AB+BD．…………………（5分）

（2）填空：如圖（3），已知等邊△ABC內(nèi)接于，AB=2，

? D為上 一點， ，AE⊥BD與點E，則△BDC

的長是? ? ．

20．解答：（1）方案A：函數(shù)表達式為．………………………（1分）

? 方案B：函數(shù)表達式為………………………（2分）

（2）由題意，得．………………………（3分）

? 解不等式，得x<2500? ………………………（4分）

∴當購買量x的取值范圍為時，選用方案A

比方案B付款少．………………………（5分）

（3）他應選擇方案B． ………………………（7分）

21．解答：過點A作，垂足為G．…………（1分）

則，在Rt中，

．…………（2分）

由題意，得．…………（3分）

（cm）．…（4分）

連接FD并延長與BA的延長線交于點H．…（5分）

由題意，得．在Rt中，

．……………………（6分）

．………（7分）

在Rt中，（cm）．……………（9分）

答：支撐角鋼CD的長為45cm，EF的長為cm．……………………（10分）

22．解答：（1）菱形

? （2）證明：作于點E．…………………………………………（3分）

由旋轉得，．

四邊形ABCD是菱形，，，，，同理，，又， 四邊形是平行四邊形，…………………（4分）

又，，，

∴四邊形是矩形…………………………………………（5分）

（3）過點B作，垂足為F，，

? ．

? 在Rt 中，，

在和中，， ．

? ∽，，即，解得，

，，．…………………（7分）

當四邊形恰好為正方形時，分兩種情況：

①點在邊上．．…………………（8分）

②點在邊的延長線上，．……………（9分）

綜上所述，a的值為或．

（4）：答案不唯一．

? 例：畫出正確圖形．……………………………………（10分）

平移及構圖方法：將沿著射線CA方向平移，平移距離為的長度，得到，

連接．………………………（11分）

結論：四邊形是平行四邊形……（12分）

23．解答：（1）拋物線經(jīng)過點A（－2，0），D（6，－8），

解得…………………………………（1分）

拋物線的函數(shù)表達式為……………………………（2分）

，拋物線的對稱軸為直線．又拋物線與x軸交于A，B兩點，點A的坐標為（－2，0）．點B的坐標為（8，0）…………………（4分）

設直線l的函數(shù)表達式為．點D（6，－8）在直線l上，6k=－8，解得．

直線l的函數(shù)表達式為………………………………………………………（5分）

點E為直線l和拋物線對稱軸的交點．點E的橫坐標為3，縱坐標為，即點E的坐標為（3，－4）……………………………………………………………………（6分）

（2）拋物線上存在點F，使≌．

點F的坐標為（）或（）．……………………………………（8分）

（3）解法一：分兩種情況：

①當時，是等腰三角形．

點E的坐標為（3，－4），，過點E作直線ME//PB，交y軸于點M，交x軸于點H，則，……………………………………（9分）

點M的坐標為（0，－5）．

設直線ME的表達式為，，解得，ME的函數(shù)表達式為，令y=0，得，解得x=15，點H的坐標為（15，0）…（10分）

又MH//PB，，即，……………………………（11分）

②當時，是等腰三角形．

當x=0時，，點C的坐標為（0，－8），

，OE=CE，，又因為，，

，CE//PB………………………………………………………………（12分）

設直線CE交x軸于點N，其函數(shù)表達式為，，解得，CE的函數(shù)表達式為，令y=0，得，，點N的坐標為

（6，0）………………………………………………………………（13分）

CN//PB，，，解得………………（14分）

綜上所述，當m的值為或時，是等腰三角形．

解法二：

當x=0時， ，點C的坐標為（0，－8），點E的坐標為

（3，－4），，，OE=CE，，設拋物線的對稱軸交直線PB于點M，交x軸于點H．分兩種情況：

①       當時，是等腰三角形．

，，CE//PB………………………………………（9分）

又HM//y軸，四邊形PMEC是平行四邊形，，

，HM//y軸，

∽，……………………………………………………（10分）

………………………………………………………（11分）

②當時，是等腰三角形．[來源:Z。xx。k.Com]

軸，∽，，……………（12分）

，，軸，∽，…………………………………………………（13分）

………………（14分）

當m的值為或時，是等腰三角形．