請點擊全屏查看
2016宜昌市中考數學模擬試題
一.選擇題
1.地球赤道半徑約為6378千米,這個數據用科學記數法表示為( )千米.
A.6.378×104????????????? B.63.78×102????????????? C.6378×10﹣4????????????? D.6.378×103
2.在﹣![]() ,﹣2,0,1這四個數中,最小的數是( )
,﹣2,0,1這四個數中,最小的數是( )
A.﹣![]() ????????????? B.﹣2????????????? C.0????????????? D.1
????????????? B.﹣2????????????? C.0????????????? D.1
3.五邊形的內角和為( )
A.360°????????????? B.540°????????????? C.720°????????????? D.900°
4.某次數學測試,“奮發有為組”學習小組6個同學按照學號順序,數學成績分別為106,98,94.102,116,85,那么這個小組這次數學測試成績的中位數是( )
A.89.5????????????? B.98????????????? C.102????????????? D.100
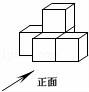
5.(2016宜昌數學)如圖是由幾個相同的小正方體搭成的一個幾何體,它的左視圖是( )
A.![]() ????????????? B.
????????????? B.![]() ????????????? C.
????????????? C.![]() ????????????? D.
????????????? D.![]()
6.一個等腰三角形的兩條邊長為3,8,那么這個等腰三角形的周長是( )
A.19????????????? B.14????????????? C.19或14????????????? D.以上均有可能
7.下列計算正確的是( )
A.a2+a3=a5????????????? B.a2?a3=a6
C.(a2)3=a5????????????? D.(﹣3x2y)3=﹣27x6y3
8.JDF學校2015年春季學期組織一次校園文化知識競賽,準備期間,擬從A,B,C,D四套卷中抽取兩套題進行模擬訓練,A卷恰好被抽中的概率是( )
A.![]() ????????????? B.
????????????? B.![]() ????????????? C.
????????????? C.![]() ????????????? D.以上都不對
????????????? D.以上都不對
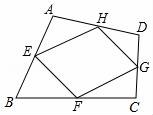
9.(2016宜昌數學)如圖,四邊形ABCD中,E,F,G,H分別是AB,BC,CD,AD邊的中點,AC=6,BD=8,那么四邊形EFGH的周長是( )
A.20????????????? B.28
C.14????????????? D.以上答案均有可能
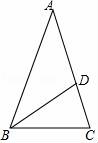
10.如圖,△ABC中,AB=AC,∠A=30°,以B為圓心,以BC為半徑畫弧交AC于點D,那么∠DBC的度數是( )
A.30°????????????? B.45°????????????? C.40°????????????? D.60°
11.(2016宜昌數學)代數式![]() 有意義,那么x的取值范圍是( )
有意義,那么x的取值范圍是( )
A.x≥1????????????? B.x≠﹣2????????????? C.x≥1且x≠﹣2????????????? D.x≠1
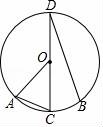
12.如圖,CD是圓O的直徑,AC,BD是弦,C是弧AB的中點,且∠BDC=25°,則∠AOC的度數是( )
A.25°????????????? B.45°????????????? C.50°????????????? D.60°
13.如圖,在4×4的網格中,將△ABC繞B順時針旋轉90°得到△BDE,則A走過的路徑的長是( )

A.π????????????? B.2π????????????? C.3π????????????? D.1.5π
14.(2016宜昌數學)如圖,點M,N在數軸上表示的數分別是m,n,則( )
![]()
A.m+n>0????????????? B.m﹣n>0????????????? C.|m|>|n|????????????? D.m2<n2
15.在同一坐標系下,y=ax2+bx和 y=﹣ax+b的圖象可能是( )
A.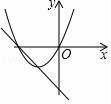 ????????????? B.
????????????? B.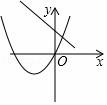 ????????????? C.
????????????? C. ????????????? D.
????????????? D.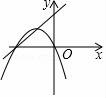
二.解答題(共9小題,計75分)
16.(6分)計算:![]() .
.
17.(6分)先化簡,![]() ÷
÷![]() ,再選一個合適的a值代入求值.
,再選一個合適的a值代入求值.
18.(2016宜昌數學)(8分)如圖,在△ABC中,
(1)請你作出AC邊上的高BD? (尺規作圖);
(2)若AB=AC=8,BC=6,求BD.
19.(8分)如圖,已知反比例函數y=![]() 與一次函數y=kx+b的圖象交于A、B兩點,且點A的橫坐標是2,點B的縱坐標是﹣2.求:
與一次函數y=kx+b的圖象交于A、B兩點,且點A的橫坐標是2,點B的縱坐標是﹣2.求:
(1)一次函數的解析式;
(2)△AOB的面積;
(3)直接寫出使反比例函數的值大于一次函數的值的x的取值范圍.
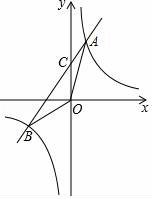
20.(8分)(2016宜昌數學)某車站在春運期間為改進服務,隨機抽樣調查了100名旅客從開始在購票窗口排隊到購到車票所用的時間t(以下簡稱購票用時,單位為分鐘).下面是這次調查統計分析得到的頻率分布表和頻率分布直方圖.解答下列問題:
分 組 |
| 頻數 | 頻率 |
一組 | 0≤t<5 | 0 | 0 |
二組 | 5≤t<10 | 10 | 0.10 |
三組 | 10≤t<15 | 10 | ?? |
四組 | 15≤t<20 | ?? | 0.50 |
五組 | 20≤t<25 | 30 | 0.30 |
合 計 | 100 | 1 | |
(1)這次抽樣的樣本容量是多少?
(2)在表中填寫出缺失的數據并補全頻率分布直方圖:
(3)旅客購票用時的平均數可能落在哪一小組?
(4)若每增加一個購票窗口可以使平均購票用時降低5分鐘,要使平均購票用時不超過10分鐘,那么請你估計最少需增加幾個窗口?
21.(2016宜昌數學)(8分)如圖,PB為⊙O的切線,B為切點,直線PO交⊙O于點E,F,過點B作PO的垂線BA,垂足為點D,交⊙O于點A,延長AO與⊙O交于點C,連接BC,AF.
(1)求證:直線PA為⊙O的切線;
(2)若BC=6,tan∠F=![]() ,求AC的長.
,求AC的長.

22.(2016宜昌數學)(9分)A市2000年時,有m萬人,每年人均用水20噸,當年庫存水量剛好供全市使用一年;到2010年時,A市有2000萬人,每年人均用水36噸,原有庫存水量不足,須從外地調水滿足需要,已知外調供水管道數為a條.預計到2020年時,與2010年相比,A市人數下降10%,每年人均用水量下降![]()
(1)預計2020年A市居民一年用水總量是多少萬噸?
(2)若A市的庫存水量保持不變,到2010年,庫存水量和a條外調供水管道供水一年的水量,剛好讓全市居民使用一年,到2020年,庫存水量和a條外調供水管道供水半年的水量,剛好滿足A市居民使用一年;如果庫存水量從2010年起,每一個10年都比前一個10年按一個相同百分數n增加,這樣2020年比2010年的外調水量將減少94%,求百分數n.
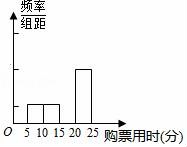
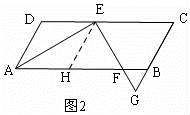
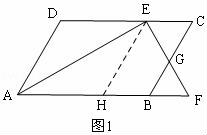
23.(10分)如圖,?ABCD中,AB=8,∠DAB的平分線交邊CD于E(點E不與A,D重合),過點E作AE的垂線交BC所在直線于點G,交AB所在直線于點F.
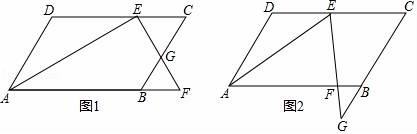
(1)當點G在CB的延長線上時(如圖2),判斷△BFG是什么三角形?說明理由.如果點G在B,C之間時此結論是否仍然成立?(不必說明理由)
(2)當點G在B,C之間時(如圖1),求AD的范圍;
(3)當2BG=BC時,求AD的長度.
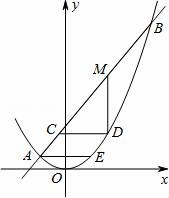
24.(2016宜昌數學)(12分)拋物線y=ax2和直線y=kx+b(k為正常數)交于點A和點B,其中點A的坐標是(﹣2,1),過點A作x軸的平行線交拋物線于點E,點D是拋物線上B.E之間的一個動點,設其橫坐標為t,經過點D作兩坐標軸的平行線分別交直線AB于點C.B,設CD=r,MD=m.
(1)根據題意可求出a= ?? ,點E的坐標是 ?? .
(2)當點D可與B、E重合時,若k=0.5,求t的取值范圍,并確定t為何值時,r的值最大;
(3)當點D不與B、E重合時,若點D運動過程中可以得到r的最大值,求k的取值范圍,并判斷當r為最大值時m的值是否最大,說明理由.(下圖供分析參考用)
2016宜昌市中考數學模擬試題
參考答案與試題解析
一.(2016宜昌數學)選擇題
1.地球赤道半徑約為6378千米,這個數據用科學記數法表示為( )千米.
A.6.378×104????????????? B.63.78×102????????????? C.6378×10﹣4????????????? D.6.378×103
【考點】1I:科學記數法—表示較大的數.
【分析】科學記數法的表示形式為a×10n的形式,其中1≤|a|<10,n為整數.確定n的值時,要看把原數變成a時,小數點移動了多少位,n的絕對值與小數點移動的位數相同.當原數絕對值>1時,n是正數;當原數的絕對值<1時,n是負數.
【解答】解:6378千米,這個數據用科學記數法表示為6.378×103千米,
故選:D.
【點評】此題考查科學記數法的表示方法.科學記數法的表示形式為a×10n的形式,其中1≤|a|<10,n為整數,表示時關鍵要正確確定a的值以及n的值.
2.在﹣![]() ,﹣2,0,1這四個數中,最小的數是( )
,﹣2,0,1這四個數中,最小的數是( )
A.﹣![]() ????????????? B.﹣2????????????? C.0????????????? D.1
????????????? B.﹣2????????????? C.0????????????? D.1
【考點】2A:實數大小比較.
【分析】根據實數的大小比較法則比較即可.
【解答】解:在﹣![]() ,﹣2,0,1這四個數中,最小的數是﹣2,
,﹣2,0,1這四個數中,最小的數是﹣2,
故選B.
【點評】本題考查了實數的大小比較法則,能熟記法則的內容是解此題的關鍵.
3.五邊形的內角和為( )
A.360°????????????? B.540°????????????? C.720°????????????? D.900°
【考點】L3:多邊形內角與外角.
【分析】n邊形的內角和是(n﹣2)180°,由此即可求出答案.
【解答】解:五邊形的內角和是(5﹣2)×180°=540°.故選B.
【點評】本題主要考查了多邊形的內角和公式,是需要熟記的內容.
4.某次數學測試,“奮發有為組”學習小組6個同學按照學號順序,數學成績分別為106,98,94.102,116,85,那么這個小組這次數學測試成績的中位數是( )
A.89.5????????????? B.98????????????? C.102????????????? D.100
【考點】W4:中位數.
【分析】根據中位數的定義先把這組數據從小到大排列,再求出最中間兩個數的平均數即可.
【解答】解:把這組數據從小到大排列為:85、94、98、102、106、116,
最中間兩個數的平均數是:(98+102)÷2=100;
故選D.
【點評】此題考查了中位數,中位數是將一組數據從小到大(或從大到小)重新排列后,最中間的那個數(最中間兩個數的平均數),叫做這組數據的中位數,解答時應先排序,熟練掌握中位數的概念是本題的關鍵.
5.(2016宜昌數學)如圖是由幾個相同的小正方體搭成的一個幾何體,它的左視圖是( )

A.![]() ????????????? B.
????????????? B.![]() ????????????? C.
????????????? C.![]() ????????????? D.
????????????? D.![]()
【考點】U2:簡單組合體的三視圖.
【分析】找到從左面看所得到的圖形即可.
【解答】解:從物體左面看,左邊2列,右邊是1列.故選A.
【點評】本題考查了三視圖的知識,左視圖是從物體的左面看得到的視圖,解答時學生易將三種視圖混淆而錯誤的選其它選項.
6.(2016宜昌數學)一個等腰三角形的兩條邊長為3,8,那么這個等腰三角形的周長是( )
A.19????????????? B.14????????????? C.19或14????????????? D.以上均有可能
【考點】KH:等腰三角形的性質;K6:三角形三邊關系.
【分析】題目給出等腰三角形有兩條邊長為8和3,而沒有明確腰、底分別是多少,所以要進行討論,還要應用三角形的三邊關系驗證能否組成三角形.
【解答】解:當腰為8時,周長=8+8+3=19;
當腰長為3時,根據三角形三邊關系可知此情況不成立;
根據三角形三邊關系可知:等腰三角形的腰長只能為8,這個三角形的周長是19.
故選:A.
【點評】本題考查了等腰三角形的性質和三角形的三邊關系;已知沒有明確腰和底邊的題目一定要想到兩種情況,分類進行討論,還應驗證各種情況是否能構成三角形進行解答,這點非常重要,也是解題的關鍵.
7.下列計算正確的是( )
A.a2+a3=a5????????????? B.a2?a3=a6
C.(a2)3=a5????????????? D.(﹣3x2y)3=﹣27x6y3
【考點】47:冪的乘方與積的乘方;24:立方根;35:合并同類項;46:同底數冪的乘法.
【分析】結合冪的乘方與積的乘方、同底數冪的乘法的概念和運算法則進行求解即可.
【解答】解:A、a2+a3≠a5,計算錯誤,不符合題意;
B、a2?a3=a5≠a6,計算錯誤,不符合題意;
C、(a2)3=a6≠a5,計算錯誤,不符合題意;
D、(﹣3x2y)3=﹣27x6y3,計算正確,符合題意.
故選D.
【點評】本題考查了冪的乘方與積的乘方、同底數冪的乘法,解答本題的關鍵在于熟練掌握各知識點的概念和運算法則.
8.(2016宜昌數學)JDF學校2015年春季學期組織一次校園文化知識競賽,準備期間,擬從A,B,C,D四套卷中抽取兩套題進行模擬訓練,A卷恰好被抽中的概率是( )
A.![]() ????????????? B.
????????????? B.![]() ????????????? C.
????????????? C.![]() ????????????? D.以上都不對
????????????? D.以上都不對
【考點】X4:概率公式.
【分析】根據題意先畫出圖形,再根據概率公式即可得出答案.
【解答】解:根據題意畫圖如下:
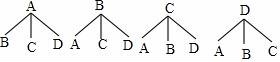
∵一共有12種情況,A卷恰好被抽中的有4種情況,
∴A卷恰好被抽中的概率是![]() =
=![]() ;
;
故選A.
【點評】本題考查了概率的知識.用到的知識點為:概率=所求情況數與總情況數之比.
9.(2016宜昌數學)如圖,四邊形ABCD中,E,F,G,H分別是AB,BC,CD,AD邊的中點,AC=6,BD=8,那么四邊形EFGH的周長是( )
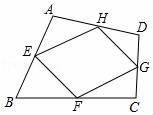
A.20????????????? B.28
C.14????????????? D.以上答案均有可能
【考點】LN:中點四邊形.
【分析】直接利用三角形中位線定理得出EH![]()
![]() BD,FG
BD,FG![]()
![]() BD,HG
BD,HG![]()
![]() AC,EF
AC,EF![]()
![]() AC,即可得出答案.
AC,即可得出答案.
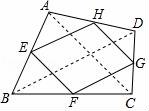
【解答】解:連接AC,BD,
∵E,F,G,H分別是AB,BC,CD,AD邊的中點,
∴EH![]()
![]() BD,FG
BD,FG![]()
![]() BD,HG
BD,HG![]()
![]() AC,EF
AC,EF![]()
![]() AC,
AC,
∴四邊形EFGH的周長是:![]() (BD+BD+AC+AC)=
(BD+BD+AC+AC)=![]() ×28=14.
×28=14.
故選:C.
【點評】此題主要考查了中點四邊形,正確把握三角形中位線的性質性質是解題關鍵.
10.(2016宜昌數學)如圖,△ABC中,AB=AC,∠A=30°,以B為圓心,以BC為半徑畫弧交AC于點D,那么∠DBC的度數是( )
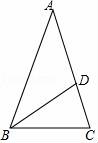
A.30°????????????? B.45°????????????? C.40°????????????? D.60°
【考點】KH:等腰三角形的性質.
【分析】在△ABC中可求得∠ACB=∠ABC=75°,在△BCD中可求得∠DBC=45°,可求出∠ABD.
【解答】解:∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
又∵BC=BD,
∴∠BDC=∠BCD=75°,
∴∠DBC=30°,
∴∠ABD=∠ABC﹣∠DBC=75°﹣30°=45°,
故選D.
【點評】本題主要考查等腰三角形的性質,掌握等邊對等角是解題的關鍵,注意三角形內角和定理的應用.
11.代數式![]() 有意義,那么x的取值范圍是( )
有意義,那么x的取值范圍是( )
A.x≥1????????????? B.x≠﹣2????????????? C.x≥1且x≠﹣2????????????? D.x≠1
【考點】72:二次根式有意義的條件.
【分析】根據被開方數是非負數,分母不能為零,可得答案.
【解答】解:由題意,得
x﹣1≥0,且x+2≠0,
∴x≥1且x≠﹣2,
故選:C,
【點評】本題考查了二次根式和分式有意義的條件,知道被開方數是非負數,分母不能為零是解題的關鍵.
12.(2016宜昌數學)如圖,CD是圓O的直徑,AC,BD是弦,C是弧AB的中點,且∠BDC=25°,則∠AOC的度數是( )

A.25°????????????? B.45°????????????? C.50°????????????? D.60°
【考點】M5:圓周角定理.
【分析】根據在同圓或等圓中,同弧或等弧所對的圓周角相等,都等于這條弧所對的圓心角的一半可得∠AOC=2∠CDB,進而可得答案.
【解答】解:∵C是弧AB的中點,
∴![]() =
=![]() ,
,
∴∠AOC=2∠CDB,
∵∠BDC=25°,
∴∠AOC=50°,
故選:C.
【點評】此題主要考查了圓周角定理,關鍵是掌握在同圓或等圓中,同弧或等弧所對的圓周角相等,都等于這條弧所對的圓心角的一半.
13.(2016宜昌數學)如圖,在4×4的網格中,將△ABC繞B順時針旋轉90°得到△BDE,則A走過的路徑的長是( )

A.π????????????? B.2π????????????? C.3π????????????? D.1.5π
【考點】O4:軌跡;R2:旋轉的性質.
【分析】由每個小正方形的邊長都為1,可求得AB長,然后由弧長公式,求得答案.
【解答】解:∵每個小正方形的邊長都為1,
∴AB=4,
∵將△ABC繞點B順時針旋轉90°得到△BDE,
∴∠ABE=90°,
∴A點運動的路徑![]() 的長為:
的長為:![]() =2π.
=2π.
故選B.
【點評】此題考查了旋轉的性質以及弧長公式的應用.注意確定半徑與圓心角是解此題的關鍵.
14.(2016宜昌數學)如圖,點M,N在數軸上表示的數分別是m,n,則( )
![]()
A.m+n>0????????????? B.m﹣n>0????????????? C.|m|>|n|????????????? D.m2<n2
【考點】13:數軸;15:絕對值.
【分析】根據M、N兩點在數軸上的位置判斷出其取值范圍,再對各選項進行逐一分析即可.
【解答】解:M、N兩點在數軸上的位置可知:﹣3<m<﹣2,1<n<2,
∵m+n<O,故A錯誤;
∵m﹣n<0,故B錯誤;
∵﹣3<m<﹣2,1<n<2,
∴|m|>|n|,
故C正確;
∵﹣3<m<﹣2,1<n<2,
∴m2>n2,
故D錯誤.
故選:C.
【點評】本題考查了實數與數軸,解決本題的關鍵是根據M、N兩點在數軸上的位置判斷出其取值范圍.
15.(2016宜昌數學)在同一坐標系下,y=ax2+bx和 y=﹣ax+b的圖象可能是( )
A. ????????????? B.
????????????? B. ????????????? C.
????????????? C. ????????????? D.
????????????? D.
【考點】H2:二次函數的圖象;F3:一次函數的圖象.
【分析】根據二次函數的c值為0,確定二次函數圖象經過坐標原點,再根據a值確定出二次函數的開口方向與一次函數所經過的象限即可得解.
【解答】解:∵y=ax2+bx(a≠0),c=0,
∴二次函數經過坐標原點;
A、B根據二次函數開口向上a>0,對稱軸x=﹣![]() <0,
<0,
所以,b>0,
∴﹣a<0,b>0,
∴一次函數經過第一、三、四象限,
∴A、B錯誤;
C、D根據二次函數開口向下a<0,對稱軸x=﹣![]() <0,
<0,
所以,b>0,
∴﹣a>0,b>0,
∴一次函數經過第一、二、三象限,
∴C錯誤,D正確;
故選D.
【點評】本題考查了二次函數的圖象,一次函數的圖象,熟練掌握函數解析式的系數與圖象的關系是解題的關鍵.
二.(2016宜昌數學)解答題(共9小題,計75分)
16.計算:![]() .
.
【考點】6F:負整數指數冪;1G:有理數的混合運算.
【分析】根據有理數的混合運算,可得答案.
【解答】解:原式=﹣9﹣10×(﹣2)+16
=﹣9+20+16
=27.
【點評】本題考查了有理數的混合運算,先算乘方,再算乘除,最后算加減.
17.先化簡,![]() ÷
÷![]() ,再選一個合適的a值代入求值.
,再選一個合適的a值代入求值.
【考點】6D:分式的化簡求值.
【分析】首先把分式的分子、分母分解因式,然后進行約分,再通分相加即可化簡,最后代入能使分式有意義的a的值求解即可.
【解答】解:原式=![]() ﹣
﹣![]()
=![]() ﹣
﹣![]()
=![]()
=![]()
=![]() .
.
當a=2時,原式=![]() .
.
【點評】本題考查了分式的化簡求值,正確對分式進行通分、約分是關鍵.
18.(2016宜昌數學)如圖,在△ABC中,
(1)請你作出AC邊上的高BD? (尺規作圖);
(2)若AB=AC=8,BC=6,求BD.

【考點】N2:作圖—基本作圖;73:二次根式的性質與化簡;KQ:勾股定理.
【分析】(1)過點B作AC的垂線,交AC于點D,則BD即為所求;
(2)設AD=x,則CD=8﹣x,在Rt△ABD中,根據勾股定理可得BD2=AB2﹣AD2=82﹣x2,在Rt△BCD中,根據勾股定理可得BD2=BC2﹣CD2=62﹣(8﹣x)2,進而得到82﹣x2=62﹣(8﹣x)2,解得x的值,最后根據勾股定理即可求得BD.
【解答】解:(1)如圖所示,BD即為所求;
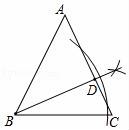
(2)設AD=x,則CD=8﹣x,
∵BD⊥AC,
∴Rt△ABD中,BD2=AB2﹣AD2=82﹣x2,
Rt△BCD中,BD2=BC2﹣CD2=62﹣(8﹣x)2,
∴82﹣x2=62﹣(8﹣x)2,
解得x=![]() ,
,
∴Rt△ABD中,BD=![]() =
=![]() =
=![]() .
.
【點評】本題主要考查了基本作圖和勾股定理的運用,解決問題的關鍵是掌握過直線外一點作已知直線的垂線的方法.解題時注意方程思想的運用.
19.(2016宜昌數學)如圖,已知反比例函數y=![]() 與一次函數y=kx+b的圖象交于A、B兩點,且點A的橫坐標是2,點B的縱坐標是﹣2.求:
與一次函數y=kx+b的圖象交于A、B兩點,且點A的橫坐標是2,點B的縱坐標是﹣2.求:
(1)一次函數的解析式;
(2)△AOB的面積;
(3)直接寫出使反比例函數的值大于一次函數的值的x的取值范圍.
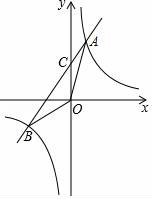
【考點】G8:反比例函數與一次函數的交點問題.
【分析】(1)由點A、B的橫縱坐標結合反比例函數解析式即可得出點A、B的坐標,再由點A、B的坐標利用待定系數法即可得出直線AB的解析式;
(2)設直線AB與y軸交于C,找出點C的坐標,利用三角形的面積公式結合A、B點的橫坐標即可得出結論;
(3)觀察函數圖象,根據圖象的上下關系即可找出不等式的解集.
【解答】解:(1)令反比例函數y=![]() ,x=2,則y=4,
,x=2,則y=4,
∴點A的坐標為(2,4);
反比例函數y=![]() 中y=﹣2,則﹣2=﹣
中y=﹣2,則﹣2=﹣![]() ,解得:x=﹣4,
,解得:x=﹣4,
∴點B的坐標為(﹣4,﹣2).
∵一次函數過A、B兩點,
∴![]() ,解得:
,解得:![]() ,
,
∴一次函數的解析式為y=x+2.
(2)設直線AB與y軸交于C,
令為y=x+2中x=0,則y=2,
∴點C的坐標為(0,2),
∴S△AOB=![]() OC?(xA﹣xB)=
OC?(xA﹣xB)=![]() ×2×[4﹣(﹣2)]=6.
×2×[4﹣(﹣2)]=6.
(3)觀察函數圖象發現:
當x<﹣4或0<x<2時,反比例函數圖象在一次函數圖象上方,
∴反比例函數的函數值大于一次函數的函數值時x的取值范圍為x<﹣4或0<x<2.
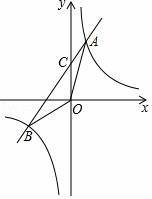
【點評】本題考查了反比例函數與一次函數的交點問題、待定系數法求函數解析式以及三角形的面積公式,解題的關鍵是:(1)求出點A、B的坐標;(2)找出點C的坐標;(3)根據函數圖象的上下關系解決不等式.本題屬于基礎題,難度不大,解決該題型題目時,找出點的坐標,再結合點的坐標利用待定系數法求出函數解析式是關鍵.
20.(2016宜昌數學)某車站在春運期間為改進服務,隨機抽樣調查了100名旅客從開始在購票窗口排隊到購到車票所用的時間t(以下簡稱購票用時,單位為分鐘).下面是這次調查統計分析得到的頻率分布表和頻率分布直方圖.解答下列問題:
分 組 |
| 頻數 | 頻率 |
一組 | 0≤t<5 | 0 | 0 |
二組 | 5≤t<10 | 10 | 0.10 |
三組 | 10≤t<15 | 10 | 0.10 |
四組 | 15≤t<20 | 50 | 0.50 |
五組 | 20≤t<25 | 30 | 0.30 |
合 計 | 100 | 1 | |
(1)這次抽樣的樣本容量是多少?
(2)在表中填寫出缺失的數據并補全頻率分布直方圖:
(3)旅客購票用時的平均數可能落在哪一小組?
(4)若每增加一個購票窗口可以使平均購票用時降低5分鐘,要使平均購票用時不超過10分鐘,那么請你估計最少需增加幾個窗口?
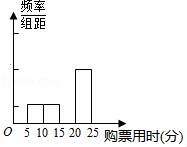
【考點】V8:頻數(率)分布直方圖;V2:全面調查與抽樣調查;V3:總體、個體、樣本、樣本容量;V7:頻數(率)分布表.
【分析】(1)根據分布表即可直接求得總數,即樣本容量;
(2)本題需先根據已知條件和樣本容量,然后根據數據和頻數與頻率之間的關系即可把表補充完整.
(3)本題根據表中所給的頻數和頻率的數據,即可得出旅客購票用時的平均數落在哪一小組內.
(4)本題需先設出旅客購票用時的平均數為t小時,再根據所要求的條件列出式子,即可求出得數.
【解答】解:(1)樣本容量是100.
(2)第5組的頻數是:100﹣30﹣10﹣10=50;
第三組的頻率是:10÷100=0.10;
分 組 |
| 頻數 | 頻率 |
一組 | 0≤t<5 | 0 | 0 |
二組 | 5≤t<10 | 10 | 0.10 |
三組 | 10≤t<15 | 10 | 0.10 |
四組 | 15≤t<20 | 50 | 0.50 |
五組 | 20≤t<25 | 30 | 0.30 |
合 計 |
| 100 | 1 |
(3)設旅客購票用時的平均數為t小時,
旅客購票用時的平均數可能落在:
15≤t<20;
∴旅客購票用時的平均數可能落在第4組.
(4)設需增加x個窗口.
則20﹣5x≤10.
∴x≥2,
∴至少需要增加2個窗口.

【點評】本題考查讀頻數分布直方圖的能力和利用統計圖獲取信息的能力;利用統計圖獲取信息時,必須認真觀察、分析、研究統計圖,才能作出正確的判斷和解決問題.
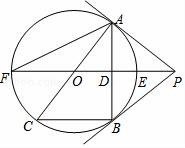
21.(2016宜昌數學)如圖,PB為⊙O的切線,B為切點,直線PO交⊙O于點E,F,過點B作PO的垂線BA,垂足為點D,交⊙O于點A,延長AO與⊙O交于點C,連接BC,AF.
(1)求證:直線PA為⊙O的切線;
(2)若BC=6,tan∠F=![]() ,求AC的長.
,求AC的長.
【考點】ME:切線的判定與性質;T7:解直角三角形.
【分析】(1)連接OB,根據垂徑定理的知識,得出OA=OB,∠POA=∠POB,繼而證明△PAO≌△PBO,然后利用全等三角形的性質結合切線的判定定理即可得出結論;
(2)根據題意可確定OD是△ABC的中位線,設AD=x,然后利用三角函數的知識表示出FD、OA,在Rt△AOD中,利用勾股定理解出x的值,根據勾股定理計算即可.
【解答】(1)證明:連接OB,
∵PB是⊙O的切線,
∴∠PBO=90°,
∵OA=OB,BA⊥PO于D,
∴AD=BD,∠POA=∠POB,
在△PAO和△PBO中,
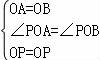 ,
,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO=90°,
∴OA⊥PA,
∴直線PA為⊙O的切線;
(2)解:∵OA=OC,AD=DB,
∴OD=![]() BC=3,
BC=3,
設AD=x,
∵tan∠F=![]() ,
,
∴FD=2x,則OA=OF=2x﹣3,
在Rt△AOD中,OA2=OD2+AD2,即(2x﹣3)2=32+x2,
解得,x=4,
則AD=4,AB=8,
∴AC=![]() =10.
=10.
【點評】(2016宜昌數學)此題考查了切線的判定與性質、勾股定理、全等三角形的判定與性質,掌握圓的切線垂直于經過切點的半徑、全等三角形的判定定理和性質定理是解題的關鍵.
22.A市2000年時,有m萬人,每年人均用水20噸,當年庫存水量剛好供全市使用一年;到2010年時,A市有2000萬人,每年人均用水36噸,原有庫存水量不足,須從外地調水滿足需要,已知外調供水管道數為a條.預計到2020年時,與2010年相比,A市人數下降10%,每年人均用水量下降![]()
(1)預計2020年A市居民一年用水總量是多少萬噸?
(2)若A市的庫存水量保持不變,到2010年,庫存水量和a條外調供水管道供水一年的水量,剛好讓全市居民使用一年,到2020年,庫存水量和a條外調供水管道供水半年的水量,剛好滿足A市居民使用一年;如果庫存水量從2010年起,每一個10年都比前一個10年按一個相同百分數n增加,這樣2020年比2010年的外調水量將減少94%,求百分數n.
【考點】AD:一元二次方程的應用.
【分析】(1)根據題意可以分別求得2020年A市的人口數和用水總量,從而可以解答本題;
(2)根據題意可以列出相應的方程組,從而可以解答本題.
【解答】解:(1)2020年A市有居民2000×(1﹣10%)=1800(萬人),
2020年A市每年人均用水36×(1﹣![]() )=30(噸),
)=30(噸),
∴2020年A市居民一年用水總量為1800×30=54000(萬噸),
答:2020年A市居民一年用水總量是54000萬噸;
(2)由題意可得,
2000年庫存水量為:20m萬噸,
設每條外調供水管道一年可以運送b噸水,
 ,
,
解得,n=27.8
答:百分數n的值是27.8.
【點評】本題考查一元二次方程的應用,解答本題的關鍵是明確題意,找出所求問題需要的條件,利用方程的思想解答.
23.(2016宜昌數學)(10分)(2016?遠安縣模擬)如圖,?ABCD中,AB=8,∠DAB的平分線交邊CD于E(點E不與A,D重合),過點E作AE的垂線交BC所在直線于點G,交AB所在直線于點F.
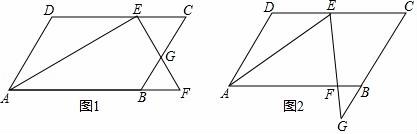
(1)當點G在CB的延長線上時(如圖2),判斷△BFG是什么三角形?說明理由.如果點G在B,C之間時此結論是否仍然成立?(不必說明理由)
(2)當點G在B,C之間時(如圖1),求AD的范圍;
(3)當2BG=BC時,求AD的長度.
【考點】LO:四邊形綜合題.
【分析】(1)如圖2,△BFG是等腰三角形,作平行線,構建菱形ADEH,證明AH=EH,所以∠EAH=∠AEH,再證明∠GFB=∠G,根據等角對等邊得:BF=BG,所以△BFG是等腰三角形;
如圖1,同理可得:△BFG是等腰三角形;
(2)由?ABCD無限接近菱形,得AD<8,點G與D點重合時,AD取最小值,由AD=AH=HB得出AD的取值范圍;
(3)分兩種情況:
①當G在邊BC上時,如圖1,根據2AD=AF=AB+BF列式計算可得AD的長;
②當G是邊CB的延長線上時,如圖2,根據AF=AB﹣BF列式可得AD的長![]() .
.
【解答】解:(1)如圖2,△BFG是等腰三角形,理由是:
過E作EH∥AD,交AB于H,
∵四邊形ABCD是平行四邊形,
∴DC∥AB,
∴四邊形ADEH是平行四邊形,
∵AE平分∠DAB,
∴∠DAE=∠EAH,
∵DC∥AB,
∴∠DEA=∠EAH,
∴∠DAE=∠DEA,
∴AD=DE,
∴?ADEH是菱形,
∴AH=EH,
∴∠EAH=∠AEH,
∵AE⊥EG,
∴∠AEG=90°,
∴∠EAH+∠HFE=90°,∠AEH+∠HEF=90°,
∴∠HEF=∠HFE,
∵EH∥AD,AD∥BC,
∴EH∥BC,
∴∠HEF=∠G,
∵∠HFE=∠GFB,
∴∠GFB=∠G,
∴BF=BG,
∴△BFG是等腰三角形;
如圖1,結論仍然成立,理由是:
過E作EH∥AD,交AB于H,
同理得:∠HEF=∠HFE,
∵EH∥BC,
∴∠HEF=∠BGF,
∴∠HFE=∠BGF,
∴BF=BG,
∴△BFG是等腰三角形;
(2)如圖1,∵若點G無限接近C點時,E點也會無限接近C點,
∴?ABCD無限接近菱形,
∴AD<8,
又∵點G與D點重合時,AD取最小值,如圖3,
過E作EH∥AD,交AB于H,
同理得:AD=AH=HB,
∴AD=![]() AB=
AB=![]() ×8=4,
×8=4,
∵點G在B,C之間,
∴AD的范圍:4<AD<8;
(3)當G在邊BC上時,如圖1,
∵BG=BF=![]() BC,AF=2AD,
BC,AF=2AD,
∴2AD=AF=AB+BF=8+![]() BC=8+
BC=8+![]() AD,
AD,
∴AD=![]() ,
,
當G是邊CB的延長線上時,如圖2,
∵BG=![]() BC,AF=2AD,BF=BG,
BC,AF=2AD,BF=BG,
∴AF=AB﹣BF=AB﹣BG,
2AD=8﹣![]() AD,
AD,
AD=![]() ,
,
綜上所述,當2BG=BC時,AD的長度的長為![]() 或
或![]() .
.

【點評】本題四邊形的綜合題,考查了平行四邊形、菱形的性質和判定,平行線的性質,等腰三角形的性質和判定,難度適中,關鍵是能作出平行線,運用了類比的解題思路,使問題得以解決.
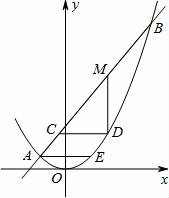
24.(12分)(2016宜昌數學)拋物線y=ax2和直線y=kx+b(k為正常數)交于點A和點B,其中點A的坐標是(﹣2,1),過點A作x軸的平行線交拋物線于點E,點D是拋物線上B.E之間的一個動點,設其橫坐標為t,經過點D作兩坐標軸的平行線分別交直線AB于點C.B,設CD=r,MD=m.
(1)根據題意可求出a= ![]() ,點E的坐標是 (2,1) .
,點E的坐標是 (2,1) .
(2)當點D可與B、E重合時,若k=0.5,求t的取值范圍,并確定t為何值時,r的值最大;
(3)當點D不與B、E重合時,若點D運動過程中可以得到r的最大值,求k的取值范圍,并判斷當r為最大值時m的值是否最大,說明理由.(下圖供分析參考用)
【考點】HF:二次函數綜合題.
【分析】(1)利用二次函數圖象上點的坐標特征知,點A的坐標滿足拋物線的解析式,所以把點A的坐標代入拋物線的解析式,即可求得a的值;由拋物線y=ax2的對稱性知,點A、點E關于y軸對稱;
(2)根據拋物線與直線的解析式求得點B的坐標為(4,4),則t的最小值是點E的橫坐標,t的最大值是點B的橫坐標;由于點C在直線y=![]() x+2上,點D在拋物線y=
x+2上,點D在拋物線y=![]() x2上,CD∥x軸,所以D(t,
x2上,CD∥x軸,所以D(t,![]() t2),C(
t2),C(![]() ,
,![]() t2);最后由兩點間的距離公式求得r=|
t2);最后由兩點間的距離公式求得r=|![]() (t﹣1)2﹣
(t﹣1)2﹣![]() |(2≤t≤4),所以根據二次函數最值的求法來求當r取最大值時t的值;
|(2≤t≤4),所以根據二次函數最值的求法來求當r取最大值時t的值;
(3)①設D(t,![]() t2).由一次函數、二次函數圖象上點的坐標特征求得點C的坐標為(
t2).由一次函數、二次函數圖象上點的坐標特征求得點C的坐標為(![]() t2﹣
t2﹣![]() ,
,![]() t2).然后根據兩點間的距離公式知r=﹣
t2).然后根據兩點間的距離公式知r=﹣![]() (t﹣2k)2+k+
(t﹣2k)2+k+![]() ,易知當t=2k時,r取最大值.
,易知當t=2k時,r取最大值.
②根據一次函數y=kx+b中的k的幾何意義知k=![]() =
=![]() ,即m=kr=﹣
,即m=kr=﹣![]() (t﹣2k)2+k2+b,顯然,當t=2k時,m取最大值.
(t﹣2k)2+k2+b,顯然,當t=2k時,m取最大值.
【解答】解:(1)根據題意知,點A(﹣2,1)在拋物線y=ax2上,
∴1=(﹣2)2a,
解得,a=![]() .
.
∵拋物線y=ax2關于y軸對稱,AE∥x軸,
∴點A、E關于y軸對稱,
∴E(2,1).
故答案是:![]() ,(2,1).
,(2,1).
(2)∵點A(﹣2,1)在直線y=kx+b(k為正常數)上,k=0.5,
∴1=﹣2×0.5+b,
解得,b=2,
即直線AB的解析式為y=![]() x+2.
x+2.
∵由(1)知,拋物線的解析式y=![]() x2,拋物線y=
x2,拋物線y=![]() x2和直線y=
x2和直線y=![]() x+2(k為正常數)交于點A和點B,
x+2(k為正常數)交于點A和點B,
∴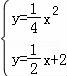 ,
,
解得,![]() 或
或![]() ,
,
∴它們的交點坐標是(﹣2,1),(4,4),即B(4,4).
當點D與點E重合時,t=2.當點D與點B重合時,t=4,
∴t的取值范圍是:2≤t≤4.
∵點C在直線y=![]() x+2上,點D在拋物線y=
x+2上,點D在拋物線y=![]() x2上,CD∥x軸,
x2上,CD∥x軸,
∴D(t,![]() t2),C(
t2),C(![]() ,
,![]() t2),
t2),
∴r=t﹣![]() =﹣
=﹣![]() (t﹣1)2+
(t﹣1)2+![]() (2≤t≤4).
(2≤t≤4).
∵在2≤t≤4范圍內,r隨t的增大而減小,
∴當t=2時,r最大=4.即當t=2時,r取最大值.
(3)∵點A、B是直線與拋物線的交點,
∴kx+b=![]() x2,即x2﹣4kx﹣4b=0,
x2,即x2﹣4kx﹣4b=0,
∴xA+xB=4k.
∵xA=﹣2,
∴xB=4k+2.
又∵點D不與B、E重合,
∴2<t<4k+2.
設D(t,![]() t2),則點C的縱坐標為
t2),則點C的縱坐標為![]() t2,將其代入y=kx+b中,得x=
t2,將其代入y=kx+b中,得x=![]() t2﹣
t2﹣![]() ,
,
∴點C的坐標為(![]() t2﹣
t2﹣![]() ,
,![]() t2),
t2),
∴r=CD=t﹣(![]() t2﹣
t2﹣![]() )=﹣
)=﹣![]() (t﹣2k)2+k+
(t﹣2k)2+k+![]() ,
,
當t=2k時,r取最大值.
∴2<2k<4k+2,
解得,k>1.
又∵k=![]() =
=![]() ,
,
∴m=kr=﹣![]() (t﹣2k)2+k2+b,
(t﹣2k)2+k2+b,
∴當t=2k時,m的值也最大.
綜上所述,當r為最大值時m的值也是最大.

【點評】本題考查了二次函數綜合題.其中涉及到的知識點由待定系數法求一次函數、二次函數的解析式,一次函數(二次函數)圖象上點的坐標特征,二次函數最值的求法等.求二次函數最值時,此題采用了“配方法”.

孔乙己是貧困潦倒的知識分子。在書中,孔乙己是一個知識分子,滿口“之乎者也”,但是他很窮,還竊書,說過“讀書人的事,怎么能叫竊,”被人嘲笑,他...

自然界產生氧氣的化學方程式:光合作用的反應式為6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反應和暗反應兩個過程。需要具備光...

有的高校沒有條件,只要學業水平成績都合格就可以,比如中國科學院大學。有的需要平常學習考試成績,比如北京外國語大學要求高三第一學期期末成績在全...

在四則運算中,表示計算順序,在小括號之后、大括號之前;表示兩個整數的最小公倍數;表示取未知數的整數部分;在函數中,表示函數的閉區間;在線性代...

濟南開設的最好的職高學校有:濟南方信集團職業高中、濟南公共交通職業高中。濟南市公共交通職業高級中學是由濟南市公共交通總公司承辦,業務屬濟南市...

實然:是說事物實際上就是這樣的,但不同于現實性(現實性指其有合理性和客觀性);應然:就是應該是怎么樣的意思,比如說這件事,就應該是那樣的結果...

地中海氣候一種夏季炎熱干燥、冬季溫和多雨,雨熱不同期的氣候類型。地中海氣候冬季受西風帶控制,鋒面氣旋頻繁活動,氣候溫和,最冷月的氣溫在4-1...

堿石灰,又稱鈉石灰,堿石灰是白色或米黃色粉末,疏松多孔,是氧化鈣(CaO,大約75%),水(H?O,大約20%),氫氧化鈉(NaOH,大約3...