各位同學(xué)在查看時(shí)請點(diǎn)擊全屏查看

2018年呂梁中考數(shù)學(xué)二次函數(shù)專項(xiàng)訓(xùn)練

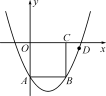
1．如圖，在平面直角坐標(biāo)系xOy中，正方形OABC的邊長為2，點(diǎn)A，C分別在y軸的負(fù)半軸和x軸的正半軸上，拋物線y＝ax2＋bx＋c經(jīng)過點(diǎn)A，B和D(4，－)，求拋物線的解析式．

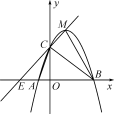
2．如圖，二次函數(shù)y＝ax2＋bx＋c的圖象與x軸交于A，B兩點(diǎn)，其中點(diǎn)A(－1，0)，點(diǎn)C(0，5)，D(1，8)都在拋物線上，M為拋物線的頂點(diǎn)．

(1)求拋物線的函數(shù)解析式；

(2)求直線CM的解析式；

(3)求△MCB的面積．

3．已知一個(gè)二次函數(shù)，當(dāng)x＝1時(shí)，y有最大值8，其圖象的形狀、開口方向與拋物線y＝－2x2相同，則這個(gè)二次函數(shù)的解析式是(?? )

A．y＝－2x2－x＋3???? B．y＝－2x2＋4

C．y＝－2x2＋4x＋8??? D．y＝－2x2＋4x＋6

4．已知某二次函數(shù)的最大值為2，圖象的頂點(diǎn)在直線y＝x＋1上，并且圖象經(jīng)過點(diǎn)(2，1)，求二次函數(shù)的解析式．

5．已知二次函數(shù)y＝ax2＋bx＋c的x與y的部分對應(yīng)值如下表：

(1)求此二次函數(shù)的解析式；

(2)畫出此函數(shù)圖象；

(3)結(jié)合函數(shù)圖象，當(dāng)－4＜x≤1時(shí)，寫出y的取值范圍．

6．已知一個(gè)二次函數(shù)的圖象經(jīng)過點(diǎn)A(－1，0)，B(3，0)和C(0，－3)三點(diǎn)；

(1)求此二次函數(shù)的解析式；

(2)對于實(shí)數(shù)m，點(diǎn)M(m，－5)是否在這個(gè)二次函數(shù)的圖象上？說明理由．

7．已知拋物線在x軸上截得的線段長是4，對稱軸是x＝－1，且過點(diǎn)(－2，－6)，求該拋物線的解析式．

8．已知y＝x2＋bx＋c的圖象向右平移2個(gè)單位長度，再向下平移3個(gè)單位長度，得到的圖象對應(yīng)的函數(shù)解析式為y＝x2－2x－3.

(1)b＝____，c＝____；

(2)求原函數(shù)圖象的頂點(diǎn)坐標(biāo)；

(3)求兩個(gè)圖象頂點(diǎn)之間的距離．

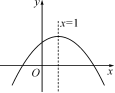
9．如圖，已知拋物線y＝－x2＋bx＋c的對稱軸為直線x＝1，且與x軸的一個(gè)交點(diǎn)為(3，0)，

那么它對應(yīng)的函數(shù)解析式是???????????????? ．

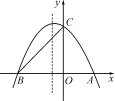
10．如圖，拋物線與x軸交于A，B兩點(diǎn)，與y軸交于C點(diǎn)，點(diǎn)A的坐標(biāo)為(2，0)，點(diǎn)C的坐標(biāo)為(0，3)，它的對稱軸是直線x＝－.

(1)求拋物線的解析式；

(2)M是線段AB上的任意一點(diǎn)，當(dāng)△MBC為等腰三角形時(shí)，

求M點(diǎn)的坐標(biāo)．

2018年呂梁中考數(shù)學(xué)二次函數(shù)專項(xiàng)訓(xùn)練參考答案

1. 解：y＝x2－x－2

2. 解：(1)y＝－x2＋4x＋5

(2)y＝－x2＋4x＋5＝－(x－2)2＋9，則M點(diǎn)坐標(biāo)為(2，9)，

可求直線MC的解析式為y＝2x＋5

(3)把y＝0代入y＝2x＋5得2x＋5＝0，解得x＝－，則E點(diǎn)坐標(biāo)為(－，0)，把y＝0代入y＝－x2＋4x＋5得－x2＋4x＋5＝0，

解得x1＝－1，x2＝5，則B點(diǎn)坐標(biāo)為(5，0)，

所以S△MCB＝S△MBE－S△CBE＝××9－××5＝15

3. D

4. 解：∵函數(shù)的最大值是2，則此函數(shù)頂點(diǎn)的縱坐標(biāo)是2，又頂點(diǎn)在y＝x＋1上，那么頂點(diǎn)的橫坐標(biāo)是1，設(shè)此函數(shù)的解析式是y＝a(x－1)2＋2，再把(2，1)代入函數(shù)中可得a(2－1)2＋2＝1，解得a＝－1，故函數(shù)解析式是y＝－(x－1)2＋2，即y＝－x2＋2x＋1

5. 解：(1)由表知，拋物線的頂點(diǎn)坐標(biāo)為(－1，4)，

設(shè)y＝a(x＋1)2＋4，把(0，3)代入得a(0＋1)2＋4＝3，

解得a＝－1，∴拋物線的解析式為y＝－(x＋1)2＋4，

即y＝－x2－2x＋3　

(2)圖象略

(3)－5＜y≤4

6. 解：(1)設(shè)二次函數(shù)的解析式為y＝a(x＋1)(x－3)，由于拋物線的圖象經(jīng)過C(0，－3)，則有－3＝a(0＋1)(0－3)，解得a＝1，∴二次函數(shù)的解析式為y＝(x＋1)(x－3)，即y＝x2－2x－3

(2)由(1)可知y＝x2－2x－3＝(x－1)2－4，則y的最小值為－4＞－5，因此無論m取何值，點(diǎn)M都不在這個(gè)二次函數(shù)的圖象上

7. 解：∵拋物線的對稱軸為x＝－1，在x軸上截得的線段長為4，∴拋物線與x軸的交點(diǎn)坐標(biāo)為(－3，0)，(1，0)，設(shè)拋物線解析式為y＝a(x＋3)(x－1)，把(－2，－6)代入得a·(－2＋3)·(－2－1)＝－6，解得a＝2，所以拋物線解析式為y＝2(x＋3)(x－1)，即y＝2x2＋4x－6

8. (1) 2??? 0

(2)(－1，－1)　

(3)由平移知兩個(gè)圖象頂點(diǎn)之間的距離＝＝

9. y＝－x2＋2x＋3

10. 解：(1)y＝－x2－x＋3

(2)由y＝0得－(x＋)2＋＝0，解得x1＝2，x2＝－3，

∴B(－3，0)．①當(dāng)CM＝BM時(shí)，∵BO＝CO＝3，即△BOC是等腰直角三角形，∴當(dāng)M點(diǎn)在原點(diǎn)O時(shí)，△MBC是等腰三角形，∴M點(diǎn)坐標(biāo)為(0，0)；②當(dāng)BC＝BM時(shí)，在Rt△BOC中，BO＝CO＝3，由勾股定理得BC＝＝3，∴BM＝3，∴M點(diǎn)坐標(biāo)(3－3，0)．

綜上所述，M點(diǎn)坐標(biāo)為(3－3，0)或(0，0)

1