各位同學在查看時請點擊全屏查看
2018年六盤水中考數(shù)學沖刺試題
一、 選擇題
1、 數(shù)![]() 中最大的數(shù)是()
中最大的數(shù)是()
A、![]() ????? B、
????? B、![]() ???? C、
???? C、![]() ????? D、
????? D、![]()
2、9的立方根是()
A、![]() ?? B、3?? C、
?? B、3?? C、![]() ? D、
? D、![]()
3、已知一元二次方程![]() 的兩根
的兩根![]() 、
、![]() ,則
,則![]() ()
()
A、4?? B、3??? C、-4??? D、-3
4、如圖是某幾何題的三視圖,下列判斷正確的是()
A、幾何體是圓柱體,高為2????? B、幾何體是圓錐體,高為2???????????????????
C、幾何體是圓柱體,半徑為2??? D、幾何體是圓柱體,半徑為2
5、若![]() ,則下列式子一定成立的是()
,則下列式子一定成立的是()
 A、
A、![]() ???? B、
???? B、![]() ???? C、
???? C、![]() ???? D、
???? D、![]()
6、如圖AB∥DE,∠ABC=20°,∠BCD=80°,則∠CDE=()
A、20°?? B、80°?? C、60°?? D、100°
7、已知AB、CD是⊙O的直徑,則四邊形ACBD是()
A、正方形??? B、矩形???? C、菱形????? D、等腰梯形
8、不等式組![]() 的整數(shù)解有()
的整數(shù)解有()
A、0個??? B、5個??? C、6個??? D、無數(shù)個
9、已知點![]() 是反比例函數(shù)
是反比例函數(shù)![]() 圖像上的點,若
圖像上的點,若![]() ,
,
則一定成立的是()
A、![]() ?? B、
?? B、![]() ??
??
C、![]() ???? D、
???? D、![]()
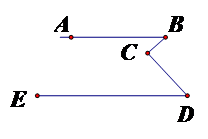
10、如圖,⊙O和⊙O′相交于A、B兩點,且OO’=5,OA=3, O’B=4,則AB=( )
A、5??? B、2.4??? C、2.5???? D、4.8
 二、填空題
二、填空題
11、正五邊形的外角和為???????????
12、計算:![]() ???????????
???????????
13、分解因式:![]() ???????????
???????????
14、如圖,某飛機于空中A處探測到目標C,此時飛行高度AC=1200米,從飛機上看地面控制點B 的俯角![]() ,則飛機A到控制點B的距離約為??????????? 。(結(jié)果保留整數(shù))
,則飛機A到控制點B的距離約為??????????? 。(結(jié)果保留整數(shù))
15、如圖,隨機閉合開關(guān)A、B、C中的一個,燈泡發(fā)光的概率為???????????
16、已知![]() ,則
,則![]() ???????????
???????????
三、解答題
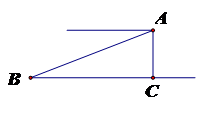
17、已知點P(-2,3)在雙曲線![]() 上,O為坐標原點,連接OP,求k的值和線段OP的長
上,O為坐標原點,連接OP,求k的值和線段OP的長
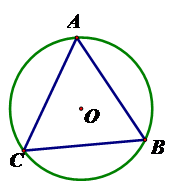
18、如圖,⊙O的半徑為2,![]() ,∠C=60°,求
,∠C=60°,求![]() 的長
的長
19、觀察下列式子
(1)根據(jù)上述規(guī)律,請猜想,若n為正整數(shù),則n=?????????????????
(2)證明你猜想的結(jié)論。
20、某校初三(1)班的同學踴躍為“雅安蘆山地震”捐款,根據(jù)捐款情況(捐款數(shù)為正數(shù))制作以下統(tǒng)計圖表,但生活委員不小心把墨水滴在統(tǒng)計表上,部分數(shù)據(jù)看不清楚。
(1)全班有多少人捐款?
(2)如果捐款0~20元的人數(shù)在扇形統(tǒng)計圖中所占的圓心角為72°,那么捐款21~40元的有多少人?
捐款 |
|
0~20元 |
|
21~40元 |
|
41~60元 |
|
61~80元 | 6 |
81元以上 | 4 |

21、校運會期間,某班預計用90元為班級同學統(tǒng)一購買礦泉水,生活委員發(fā)現(xiàn)學校小賣部有優(yōu)惠活動:購買瓶裝礦泉水打9折,經(jīng)計算按優(yōu)惠價購買能多買5瓶,求每瓶礦泉水的原價和該班實際購買礦泉水的數(shù)量。
22、如圖,矩形OABC頂點A(6,0)、C(0,4),直線![]() 分別交BA、OA于點D、E,且D為BA中點。
分別交BA、OA于點D、E,且D為BA中點。
(1)求k的值及此時△EAD的面積;
 (2)現(xiàn)向矩形內(nèi)隨機投飛鏢,求飛鏢落在△EAD內(nèi)的概率。
(2)現(xiàn)向矩形內(nèi)隨機投飛鏢,求飛鏢落在△EAD內(nèi)的概率。
(若投在邊框上則重投)
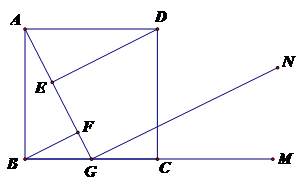
23、如圖,正方形ABCD中,G是BC中點,DE⊥AG于E,BF⊥AG于F,GN∥DE,M是BC延長線上一點。
(1)求證:△ABF≌△DAE
(2)尺規(guī)作圖:作∠DCM的平分線,交GN于點H(保留作圖痕跡,不寫作法和證明),試證明GH=AG
24、已知拋物線![]()
(1)若![]() 求該拋物線與x軸的交點坐標;
求該拋物線與x軸的交點坐標;
(2)若![]() ,是否存在實數(shù)
,是否存在實數(shù)![]() ,使得相應的y=1,若有,請指明有幾個并證明你的結(jié)論,若沒有,闡述理由。
,使得相應的y=1,若有,請指明有幾個并證明你的結(jié)論,若沒有,闡述理由。
(3)若![]() 且拋物線在
且拋物線在![]() 區(qū)間上的最小值是-3,求b的值。
區(qū)間上的最小值是-3,求b的值。

25、已知等腰![]() 和等腰
和等腰![]() 中,∠ACB=∠AED=90°,且AD=AC
中,∠ACB=∠AED=90°,且AD=AC
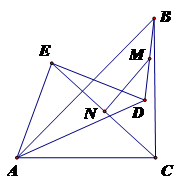
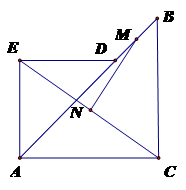
(1)發(fā)現(xiàn):如圖1,當點E在AB上且點C和點D重合時,若點M、N分別是DB、EC的中點,則MN與EC的位置關(guān)系是???????????? ,MN與EC的數(shù)量關(guān)系是????????????
(2)探究:若把(1)小題中的△AED繞點A旋轉(zhuǎn)一定角度,如圖2所示,連接BD和EC,并連接DB、EC的中點M、N,則MN與EC的位置關(guān)系和數(shù)量關(guān)系仍然能成立嗎?若成立,請以逆時針旋轉(zhuǎn)45°得到的圖形(圖3)為例給予證明位置關(guān)系成立,以順時針旋轉(zhuǎn)45°得到的圖形(圖4)為例給予證明數(shù)量關(guān)系成立,若不成立,請說明理由。
 ????
???? 
說明:
1、本解答給出了一種解法供參考,如果考生的解法與本解答不同,各題組可根據(jù)試題的主要考查內(nèi)容比照評分標準制訂相應的評分細則.
2、對于計算題,當考生的解答在某一步出現(xiàn)錯誤時,如果后續(xù)部分的解答未改變該題的內(nèi)容和難度,可視影響的程度決定給分,但不得超過該部分正確解答應得分數(shù)的一半;如果后續(xù)部分的解答有較嚴重的錯誤,就不再給分.
3、解答右端所注分數(shù),表示考生正確做到這一步應得的累加分數(shù).
一、選擇題(本題共10小題,每小題3分,共30分)
題號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | D | A | A | B | C | B | B | B | D |
二、填空題(本題共6小題,每小題3分,共18分)
題號 | 11 | 12 | 13 | 14 | 15 | 16 |
答案 | 360° | -m2 |
| 3509 |
| 2 |
三、解答題(本題有9個小題, 共102分。解答應寫出文字說明、證明過程或演算步驟)
17.(本小題滿分9分)
解:(1)把![]() 代入
代入![]() ,得
,得![]() ?? --------4分
?? --------4分
?? (2)過點P作PE⊥![]() 軸于點E,則OE=2,PE=3??? --------6分
軸于點E,則OE=2,PE=3??? --------6分
∴在![]() △OPE中, PO=
△OPE中, PO=![]() ?? --------9分
?? --------9分
18.(本小題滿分9分)
解:方法一
連接OA,OC? --------1分
∵![]() ,∠C=60°
,∠C=60°
∴∠B=60°???????? --------4分
∴ ∠AOC=120°????? --------6分
∴ ![]() π×2=
π×2=![]() π? --------9分
π? --------9分
方法二:
∵![]()
∴ ![]() ??? --------2分
??? --------2分
???? ∵∠C=60°
???? ∴ ![]() ?? --------5分
?? --------5分
???? ∴ ![]() =
=![]() ???? --------7分
???? --------7分
∴![]() =
=![]() π? --------9分
π? --------9分
19.(本題滿分10分)
(1)![]() ??????? ----------3分
??????? ----------3分
(2)證明:∵![]()
???????????? ![]() ????? ----------5分
????? ----------5分
???????????? ![]() ???????? ----------7分
???????? ----------7分
???????????? ![]() ?????? ----------8分
?????? ----------8分
???????????? ![]() ??????? ----------9分
??????? ----------9分
????? ∴ ![]() ?????? ----------10分
?????? ----------10分
20.(本題滿分10分)
解:(1)![]() ??????? ----------2分
??????? ----------2分
???????? 答:全班有50人捐款。?? ----------3分
??? (2)方法1:∵捐款0~20元的人數(shù)在扇形統(tǒng)計圖中所占的圓心角為72°
?????????? ∴捐款0~20元的人數(shù)為![]() ??? ----------6分
??? ----------6分
?????????? ∴![]() ??????? ----------9分
??????? ----------9分
????????? 答:捐款21~40元的有14人?????? ----------10分
???????? 方法2: ∵捐款0~20元的人數(shù)在扇形統(tǒng)計圖中所占的圓心角為72°
?????????? ∴捐款0~20元的百分比為![]() ??? ----------6分
??? ----------6分
?????????? ∴![]() ??????? ----------9分
??????? ----------9分
????????? 答:捐款21~40元的有14人????? ----------10分
21.(本題滿分12分)
方法1? 解:設每瓶礦泉水的原價為x元?? ----------1分
![]() ???????? ----------5分
???????? ----------5分
解得:![]() ????????? ----------8分
????????? ----------8分
經(jīng)檢驗:x=2是原方程的解???? ----------9分
∴![]() ??????? ----------11分
??????? ----------11分
答:每瓶礦泉水的原價為2元,該班實際購買礦泉水50瓶。----------12分
方法2? 解:設每瓶礦泉水的原價為x元,該班原計劃購買y瓶礦泉水?? ----------1分
![]() ?????????? ----------5分
?????????? ----------5分
解得:![]() ??????????? ----------9分
??????????? ----------9分
∴![]() ???????????? ----------11分
???????????? ----------11分
答:每瓶礦泉水的原價為2元,該班實際購買礦泉水50瓶。----------12分
22.(本小題滿分12分)
解:(1)∵矩形OABC頂點A(6,0)、C(0,4)
∴B(6,4)??????? --------1分
∵ D為BA中點
∴ D(6,2),AD=2???? --------2分
把點D(6,2)代入![]() 得k=
得k=![]() ? --------4分
? --------4分
令![]() 得
得![]()
∴ E(2,0)? --------5分
∴ OE=2,AE=4???? --------7分
∴![]() =
=![]() =
=![]() ??? --------9分
??? --------9分
(2)由(1)得![]() ??? --------10分
??? --------10分
∴ ![]() ???? --------12分
???? --------12分
23.(本題滿分12分)
解:∵ 四邊形ABCD是正方形
∴ AB=BC=CD=DA ?? ----------1分
∠DAB=∠ABC=90°?
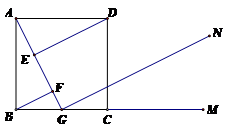 ∴ ∠DAE+∠GAB=90°?
∴ ∠DAE+∠GAB=90°?
∵ DE⊥AG?? BF⊥AG
∴ ∠AED=∠BFA=90°
∠DAE +∠ADE=90°
??? ∴ ∠GAB =∠ADE???? ----------3分
在△ABF和△DAE中

??? ∴ △ABF≌△DAE???? ----------5分
(2)作圖略?? ----------7分
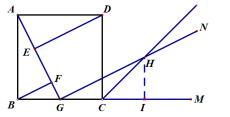 方法1:作HI⊥BM于點I? ----------8分
方法1:作HI⊥BM于點I? ----------8分
∵ GN∥DE
∴ ∠AGH=∠AED=90°
∴ ∠AGB+∠HGI=90°
∵ HI⊥BM
∴ ∠GHI+∠HGI=90°
∴ ∠AGB =∠GHI?? ----------9分
∵ G是BC中點
∴ tan∠AGB=![]()
∴ tan∠GHI= tan∠AGB=![]()
∴ GI=2HI????? ----------10分
∵ CH平分∠DCM
∴ ∠HCI=![]()
∴ CI=HI
∴ CI=CG=BG=HI??? ----------11分
在△ABG和△GIH中

∴ △ABG≌△GIH???
∴ AG=GH???? ----------12分
 方法2: 作AB中點P,連結(jié)GP?? ----------8分
方法2: 作AB中點P,連結(jié)GP?? ----------8分
∵ P、G分別是AB、BC中點 且AB=BC
∴ AP=BP=BG=CG??? ----------9分
∴ ∠BPG=45°
∵ CH平分∠DCM
∴ ∠HCM=![]()
∴ ∠APG=∠HCG=135° ----------10分
∵ GN∥DE
∴ ∠AGH=∠AED=90°
∴ ∠AGB+∠HGM=90°
∵ ∠BAG+∠AGB=90°
∴ ∠BAG =∠HGM ? ----------11分
在△AGP和△GHC中
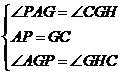
∴ △AGP≌△GHC??
∴ AG=GH????? ----------12分
24.(本題滿分14分)
解(1)當![]() ,
,![]() 時,拋物線為
時,拋物線為![]() ,
,
∵方程![]() 的兩個根為
的兩個根為![]() ,
,![]() .
.
∴該拋物線與![]() 軸公共點的坐標是
軸公共點的坐標是![]() 和
和![]() .? --------------------------------3分
.? --------------------------------3分
(2)由![]() 得
得![]() ,
,
![]()
![]() ----------------------5分
----------------------5分
![]() ,
,![]() --------------------------------7分
--------------------------------7分
所以方程![]() 有兩個不相等實數(shù)根,
有兩個不相等實數(shù)根,
即存在兩個不同實數(shù)![]() ,使得相應
,使得相應![]() .-------------------------8分
.-------------------------8分
(3)![]() ,則拋物線可化為
,則拋物線可化為![]() ,其對稱軸為
,其對稱軸為![]() ,
,
當![]() 時,即
時,即![]() ,則有拋物線在
,則有拋物線在![]() 時取最小值為-3,此時-
時取最小值為-3,此時-![]() ,解得
,解得![]() ,合題意--------------10分
,合題意--------------10分
當![]() 時,即
時,即![]() ,則有拋物線在
,則有拋物線在![]() 時取最小值為-3,此時-
時取最小值為-3,此時-![]() ,解得
,解得![]() ,不合題意,舍去.--------------12分
,不合題意,舍去.--------------12分
當![]() 時,即
時,即![]() ,則有拋物線在
,則有拋物線在![]() 時取最小值為-3,此時
時取最小值為-3,此時![]() ,化簡得:
,化簡得:![]() ,解得:
,解得:![]() (不合題意,舍去),
(不合題意,舍去),![]() . --------------14分
. --------------14分
綜上:![]() 或
或![]()
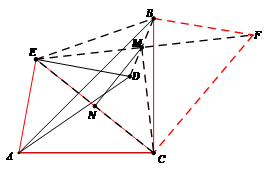
25.(本題滿分14分)
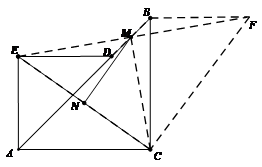 解:解:(1)
解:解:(1)![]() .------------2分
.------------2分
(2)連接EM并延長到F,使EM=MF,連接CM、CF、BF. ------------3分
∵BM=MD,∠EMD=∠BMF,
∴△EDM≌△FBM
∴BF=DE=AE,∠FBM=∠EDM=135°
∴∠FBC=∠EAC=90°---------5分
∴△EAC≌△FBC
∴FC=EC, ∠FCB=∠ECA---------6分
∴∠ECF=∠FCB+∠BCE =∠ECA+∠BCE=90°
又點M、N分別是EF、EC的中點
∴MN∥FC
∴MN⊥FC---------8分
(可把Rt△EAC繞點C旋轉(zhuǎn)90°得到Rt△CBF,連接MF,ME,MC,然后證明三點共線)
證法2:延長ED到F,連接AF、MF,則AF為矩形ACFE對角線,所以比經(jīng)過EC的中點N且AN=NF=EN=NC.----------------------------4分
在Rt△BDF中,M是BD的中點,∠B=45°
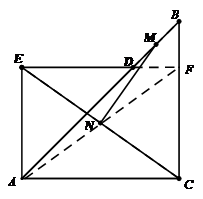 ∴FD=FB
∴FD=FB
∴FM⊥AB,
∴MN=NA=NF=NC---------------------5分
∴點A、C、F、M都在以N為圓心的圓上
∴∠MNC=2∠DAC--------------------6分
由四邊形MACF中,∠MFC=135°
∠FMA=∠ACB=90°
∴∠DAC=45°
∴∠MNC=90°即MN⊥FC-------------------8分
(還有其他證法,相應給分)
(3)連接EF并延長交BC于F,------------------9分
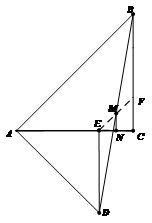 ∵∠AED=∠ACB=90°
∵∠AED=∠ACB=90°
∴DE∥BC
∴∠DEM=∠AFM,∠EDM=∠MBF
又BM=MD
∴△EDM≌△FBM-----------------11分
∴BF=DE=AE,EM=FM
∴![]() --------------14分
--------------14分
(另證:也可連接DN并延長交BC于M)
備注:任意旋轉(zhuǎn)都成立,如下圖證明兩個紅色三角形全等。其中∠EAC=∠CBF的證明,
可延長ED交BC于G,通過角的轉(zhuǎn)換得到

孔乙己是貧困潦倒的知識分子。在書中,孔乙己是一個知識分子,滿口“之乎者也”,但是他很窮,還竊書,說過“讀書人的事,怎么能叫竊,”被人嘲笑,他...

自然界產(chǎn)生氧氣的化學方程式:光合作用的反應式為6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反應和暗反應兩個過程。需要具備光...

有的高校沒有條件,只要學業(yè)水平成績都合格就可以,比如中國科學院大學。有的需要平常學習考試成績,比如北京外國語大學要求高三第一學期期末成績在全...

在四則運算中,表示計算順序,在小括號之后、大括號之前;表示兩個整數(shù)的最小公倍數(shù);表示取未知數(shù)的整數(shù)部分;在函數(shù)中,表示函數(shù)的閉區(qū)間;在線性代...

濟南開設的最好的職高學校有:濟南方信集團職業(yè)高中、濟南公共交通職業(yè)高中。濟南市公共交通職業(yè)高級中學是由濟南市公共交通總公司承辦,業(yè)務屬濟南市...

實然:是說事物實際上就是這樣的,但不同于現(xiàn)實性(現(xiàn)實性指其有合理性和客觀性);應然:就是應該是怎么樣的意思,比如說這件事,就應該是那樣的結(jié)果...

地中海氣候一種夏季炎熱干燥、冬季溫和多雨,雨熱不同期的氣候類型。地中海氣候冬季受西風帶控制,鋒面氣旋頻繁活動,氣候溫和,最冷月的氣溫在4-1...

堿石灰,又稱鈉石灰,堿石灰是白色或米黃色粉末,疏松多孔,是氧化鈣(CaO,大約75%),水(H?O,大約20%),氫氧化鈉(NaOH,大約3...