各位同學在查看時請點擊全屏查看
2018年黔東南中考數學模擬試題
一、選擇題(本題共10小題,每小題3分,共30分,只有一項符合題意要求)
1.﹣2015的相反數( )
A.﹣2015????????????? B.![]() ????????????? C.2015????????????? D.﹣
????????????? C.2015????????????? D.﹣![]()
2.下面四個幾何體中,主視圖是圓的幾何體是( )
A. ????????????? B.
????????????? B. ????????????? C.
????????????? C. ????????????? D.
????????????? D.
3.下列運算正確的是( )
A.a3?a3=a9????????????? B.(﹣3a3)2=9a6????????????? C.5a+3b=8ab????????????? D.(a+b)2=a2+b2
4.下列圖形中,是軸對稱圖形的是( )
A. ????????????? B.
????????????? B. ????????????? C.
????????????? C. ????????????? D.
????????????? D.
5.下列圖形中,單獨選用一種圖形不能進行平面鑲嵌的是( )
A.正三角形????????????? B.正六邊形????????????? C.正方形????????????? D.正五邊形
6.直尺與三角尺按如圖所示的方式疊放在一起,在圖中所標記的角中,與∠1互余的角有幾個( )
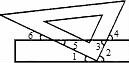
A.2個????????????? B.3個????????????? C.4個????????????? D.6個
7.在平面中,下列命題為真命題的是( )
A.四個角相等的四邊形是矩形????????????? B.對角線垂直的四邊形是菱形
C.對角線相等的四邊形是矩形????????????? D.四邊相等的四邊形是正方形
8.我省五個旅游景區門票票價如下表所示(單位:元),關于這五個景區票價的說法中,正確的是( )
景區名稱 | 黃果樹大瀑布 | 織金洞 | 玉舍森林滑雪 | 安順龍宮 | 荔波小七孔 |
票價(元) | 180 | 120 | 200 | 130 | 180 |
A.平均數126????????????? B.眾數180????????????? C.中位數200????????????? D.極差70
9.已知關于x的一元二次方程(k﹣1)x2﹣2x+1=0有兩個不相等的實數根,則k的取值范圍是( )
A.k<﹣2????????????? B.k<2????????????? C.k>2????????????? D.k<2且k≠1
10.下列圖形中,陰影部分面積最大的是( )
A.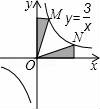 ????????????? B.
????????????? B.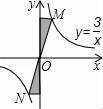 ????????????? C.
????????????? C.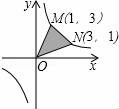 ????????????? D.
????????????? D.
二、填空題(本題8小題,每小題4分,共計32分)
11.H7N9禽流感病毒的直徑大約為0.0000000805米,用科學記數法表示為 米(保留兩位有效數字)
12.因式分解:4x3﹣36x= .
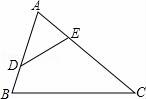
13.如圖,添加一個條件: ,使△ADE∽△ACB,(寫出一個即可)
14.在六盤水市組織的“五城聯創”演講比賽中,小明等25人進入總決賽,賽制規定,13人早上參賽,12人下午參賽,小明抽到上午比賽的概率是 .
15.如圖,梯形ABCD中,AD∥BC,AD=4,AB=5,BC=10,CD的垂直平分線交BC于E,連接DE,則四邊形ABED的周長等于 .

16.若⊙A和⊙B相切,它們的半徑分別為8cm和2cm,則圓心距AB為 cm.
17.無論x取任何實數,代數式![]() 都有意義,則m的取值范圍為 .
都有意義,則m的取值范圍為 .
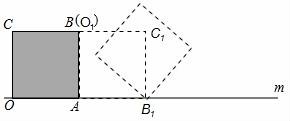
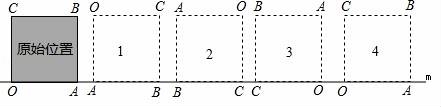
18.把邊長為1的正方形紙片OABC放在直線m上,OA邊在直線m上,然后將正方形紙片繞著頂點A按順時針方向旋轉90°,此時,點O運動到了點O1處(即點B處),點C運動到了點C1處,點B運動到了點B1處,又將正方形紙片AO1C1B1繞B1點,按順時針方向旋轉90°…,按上述方法經過4次旋轉后,頂點O經過的總路程為 ,經過61次旋轉后,頂點O經過的總路程為 .
三、解答題(本題共7個小題,共88分,解答時應寫出必要的文字說明,證明過程或演算步驟)
19.(1)![]() +(2013﹣π)0
+(2013﹣π)0
(2)先化簡,再求值:(![]() )
)![]() ,其中x2﹣4=0.
,其中x2﹣4=0.
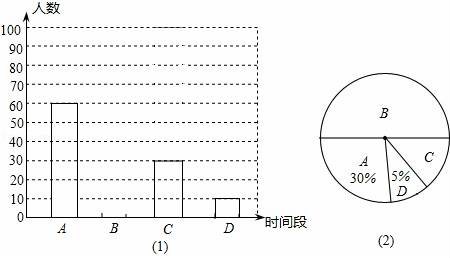
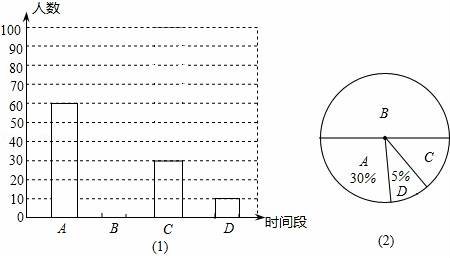
20.為了了解中學生參加體育活動的情況,某校對部分學生進行了調查,其中一個問題是:“你平均每天參加體育活動的時間是多少?”共有4個選項:
A.1.5小時以上??? B.1﹣﹣1.5小時??? C.0.5小時?? D.0.5小時以下
根據調查結果繪制了兩幅不完整的統計圖.
請你根據以上信息解答下列問題:
(1)本次調查活動采取了 調查方式.
(2)計算本次調查的學生人數和圖(2)選項C的圓心角度數.
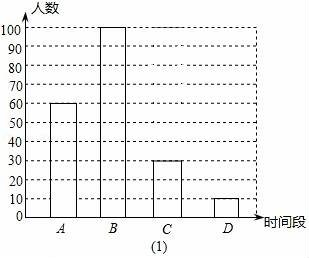
(3)請根據圖(1)中選項B的部分補充完整.
(4)若該校有3000名學生,你估計該校可能有多少名學生平均每天參加體育活動的時間在0.5小時以下.
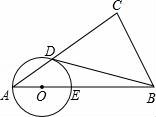
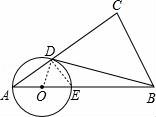
21.在Rt△ACB中,∠C=90°,點O在AB上,以O為圓心,OA長為半徑的圓與AC,AB分別交于點D,E,且∠CBD=∠A.
(1)判斷直線BD與⊙O的位置關系,并證明你的結論.
(2)若AD:AO=6:5,BC=3,求BD的長.
22.閱讀材料:
關于三角函數還有如下的公式:
sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)=![]()
利用這些公式可以將一些不是特殊角的三角函數轉化為特殊角的三角函數來求值.
例:tan15°=tan(45°﹣30°)=![]() =
= =
=![]()
根據以上閱讀材料,請選擇適當的公式解答下面問題
(1)計算:sin15°;
(2)烏蒙鐵塔是六盤水市標志性建筑物之一(圖1),小華想用所學知識來測量該鐵塔的高度,如圖2,小華站在離塔底A距離7米的C處,測得塔頂的仰角為75°,小華的眼睛離地面的距離DC為1.62米,請幫助小華求出烏蒙鐵塔的高度.(精確到0.1米,參考數據![]() ,
,![]() )
)

23.為了抓住2013年涼都消夏文化節的商機,某商場決定購進甲、乙兩種紀念品,若購進甲種紀念品1件,乙種紀念品2件,需要160元;購進甲種紀念品2件,乙種紀念品3件,需要280元.
(1)購進甲乙兩種紀念品每件各需要多少元?
(2)該商場決定購進甲乙兩種紀念品100件,并且考慮市場需求和資金周轉,用于購買這些紀念品的資金不少于6000元,同時又不能超過6430元,則該商場共有幾種進貨方案?
(3)若銷售每件甲種紀念品可獲利30元,每件乙種紀念品可獲利12元,在第(2)問中的各種進貨方案中,哪種方案獲利最大?最大利潤是多少元?
24.(1)觀察發現
?? 如圖(1):若點A、B在直線m同側,在直線m上找一點P,使AP+BP的值最小,做法如下:
?? 作點B關于直線m的對稱點B′,連接AB′,與直線m的交點就是所求的點P,線段AB′的長度即為AP+BP的最小值.
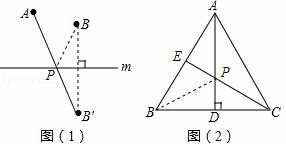
?? 如圖(2):在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小,做法如下:
作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這點就是所求的點P,故BP+PE的最小值為 .
(2)實踐運用
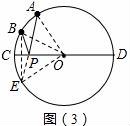
?? 如圖(3):已知⊙O的直徑CD為2,![]() 的度數為60°,點B是
的度數為60°,點B是![]() 的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的最小值為 .
的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的最小值為 .
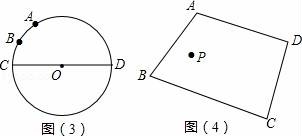
? (3)拓展延伸
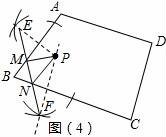
如圖(4):點P是四邊形ABCD內一點,分別在邊AB、BC上作出點M,點N,使PM+PN+MN的值最小,保留作圖痕跡,不寫作法.
25.已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=![]() ,若以O為坐標原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.
,若以O為坐標原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.
(1)求經過點O,C,A三點的拋物線的解析式.
(2)求拋物線的對稱軸與線段OB交點D的坐標.
(3)線段OB與拋物線交于點E,點P為線段OE上一動點(點P不與點O,點E重合),過P點作y軸的平行線,交拋物線于點M,問:在線段OE上是否存在這樣的點P,使得PD=CM?若存在,請求出此時點P的坐標;若不存在,請說明理由.
2018年黔東南中考數學模擬試題參考答案
一、選擇題(本題共10小題,每小題3分,共30分,只有一項符合題意要求)
1.﹣2015的相反數( )
A.﹣2015????????????? B.![]() ????????????? C.2015????????????? D.﹣
????????????? C.2015????????????? D.﹣![]()
【考點】相反數.
【分析】利用相反數的定義求解即可.
【解答】解:﹣2015的相反數是2015.
故選:C.
【點評】本題主要考查了相反數的定義,解題的關鍵是熟記相反數的定義.
2.下面四個幾何體中,主視圖是圓的幾何體是( )
A.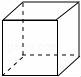 ????????????? B.
????????????? B.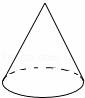 ????????????? C.
????????????? C. ????????????? D.
????????????? D.
【考點】簡單幾何體的三視圖.
【分析】根據主視圖是從物體正面看所得到的圖形,即可選出答案.
【解答】解:正方體的主視圖是正方形,圓錐的主視圖是三角形,圓柱體的主視圖是長方形,球的主視圖是圓,
故選:D.
【點評】本題考查了幾何體的三視圖,掌握定義是關鍵.注意所有的看到的棱都應表現在三視圖中.
3.下列運算正確的是( )
A.a3?a3=a9????????????? B.(﹣3a3)2=9a6????????????? C.5a+3b=8ab????????????? D.(a+b)2=a2+b2
【考點】冪的乘方與積的乘方;合并同類項;同底數冪的乘法;完全平方公式.
【專題】計算題.
【分析】A、利用同底數冪的乘法法則計算得到結果,即可作出判斷;
B、利用積的乘方與冪的乘方運算法則計算得到結果,即可作出判斷;
C、本選項不能合并,錯誤;
D、利用完全平方公式展開得到結果,即可作出判斷.
【解答】解:A、a3?a3=a6,故A錯誤;
B、(﹣3a3)2=9a6,故B正確;
C、5a+3b不能合并,故C錯誤;
D、(a+b)2=a2+2ab+b2,故D錯誤,
故選:B.
【點評】此題考查了積的乘方與冪的乘方,合并同類項,同底數冪的乘法,以及完全平方公式,熟練掌握公式及法則是解本題的關鍵.
4.下列圖形中,是軸對稱圖形的是( )
A. ????????????? B.
????????????? B. ????????????? C.
????????????? C. ????????????? D.
????????????? D.
【考點】軸對稱圖形.
【分析】根據軸對稱圖形的定義:如果一個圖形沿一條直線折疊,直線兩旁的部分能夠互相重合,這個圖形叫做軸對稱圖形,這條直線叫做對稱軸,這時,我們也可以說這個圖形關于這條直線(成軸)對稱,進而得出答案.
【解答】解:A、不是軸對稱圖形,故A錯誤;
B、是軸對稱圖形,故B正確;
C、不是軸對稱圖形,故C錯誤;
D、不是軸對稱圖形,故D錯誤.
故選:B.
【點評】本題考查了軸對稱圖形的概念.軸對稱圖形的關鍵是尋找對稱軸,圖形兩部分折疊后可重合.
5.下列圖形中,單獨選用一種圖形不能進行平面鑲嵌的是( )
A.正三角形????????????? B.正六邊形????????????? C.正方形????????????? D.正五邊形
【考點】平面鑲嵌(密鋪).
【分析】幾何圖形鑲嵌成平面的關鍵是:圍繞一點拼在一起的多邊形的內角加在一起恰好組成一個周角.360°為正多邊形一個內角的整數倍才能單獨鑲嵌.
【解答】解:A、正三角形的一個內角度數為180﹣360÷3=60°,是360°的約數,能鑲嵌平面,不符合題意;
B、正六邊形的一個內角度數為180﹣360÷6=120°,是360°的約數,能鑲嵌平面,不符合題意;
C、正方形的一個內角度數為180﹣360÷4=90°,是360°的約數,能鑲嵌平面,不符合題意;
D、正五邊形的一個內角度數為180﹣360÷5=108°,不是360°的約數,不能鑲嵌平面,符合題意.
故選:D.
【點評】本題考查了平面密鋪的知識,注意掌握只用一種正多邊形鑲嵌,只有正三角形,正四邊形,正六邊形三種正多邊形能鑲嵌成一個平面圖案.
6.直尺與三角尺按如圖所示的方式疊放在一起,在圖中所標記的角中,與∠1互余的角有幾個( )

A.2個????????????? B.3個????????????? C.4個????????????? D.6個
【考點】余角和補角.
【專題】計算題.
【分析】本題要注意到∠1與∠2互余,并且直尺的兩邊互相平行,可以考慮平行線的性質.
【解答】解:與∠1互余的角有∠2,∠3,∠4;一共3個.
故選:B.
【點評】正確觀察圖形,由圖形聯想到學過的定理是數學學習的一個基本要求.
7.在平面中,下列命題為真命題的是( )
A.四個角相等的四邊形是矩形????????????? B.對角線垂直的四邊形是菱形
C.對角線相等的四邊形是矩形????????????? D.四邊相等的四邊形是正方形
【考點】命題與定理.
【分析】分別根據矩形、菱形、正方形的判定與性質分別判斷得出即可.
【解答】解:A、根據四邊形的內角和得出,四個角相等的四邊形即四個內角是直角,故此四邊形是矩形,故A正確;
B、只有對角線互相平分且垂直的四邊形是菱形,故B錯誤;
C、對角線互相平分且相等的四邊形是矩形,故C錯誤;
D、四邊相等的四邊形是菱形,故D錯誤.
故選:A.
【點評】此題主要考查了矩形、菱形、正方形的判定與性質,正確把握相關定理是解題關鍵.
8.我省五個旅游景區門票票價如下表所示(單位:元),關于這五個景區票價的說法中,正確的是( )
景區名稱 | 黃果樹大瀑布 | 織金洞 | 玉舍森林滑雪 | 安順龍宮 | 荔波小七孔 |
票價(元) | 180 | 120 | 200 | 130 | 180 |
A.平均數126????????????? B.眾數180????????????? C.中位數200????????????? D.極差70
【考點】極差;算術平均數;中位數;眾數.
【分析】根據極差、眾數及中位數的定義,結合選項進行判斷即可.
【解答】解:將數據從小到大排列為:120,130,180,180,200,
A、平均數=![]() ×(120+130+180+180+200)=162,故A錯誤;
×(120+130+180+180+200)=162,故A錯誤;
B、眾數為180,故B正確;
C、中位數為180,故C錯誤;
D、極差為200﹣120=80,故D錯誤;
故選:B.
【點評】本題考查了中位數、眾數、平均數及極差的知識,掌握各部分的定義是關鍵,在判斷中位數的時候一樣要將數據重新排列.
9.已知關于x的一元二次方程(k﹣1)x2﹣2x+1=0有兩個不相等的實數根,則k的取值范圍是( )
A.k<﹣2????????????? B.k<2????????????? C.k>2????????????? D.k<2且k≠1
【考點】根的判別式;一元二次方程的定義.
【專題】計算題;壓軸題.
【分析】根據方程有兩個不相等的實數根,得到根的判別式的值大于0列出關于k的不等式,求出不等式的解集即可得到k的范圍.
【解答】解:根據題意得:△=b2﹣4ac=4﹣4(k﹣1)=8﹣4k>0,且k﹣1≠0,
解得:k<2,且k≠1.
故選:D.
【點評】此題考查了根的判別式,以及一元二次方程的定義,弄清題意是解本題的關鍵.
10.下列圖形中,陰影部分面積最大的是( )
A.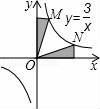 ????????????? B.
????????????? B.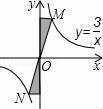 ????????????? C.
????????????? C. ????????????? D.
????????????? D.
【考點】反比例函數系數k的幾何意義.
【專題】壓軸題.
【分析】分別根據反比例函數系數k的幾何意義以及三角形面積求法以及梯形面積求法得出即可.
【解答】解:A、根據反比例函數系數k的幾何意義,陰影部分面積和為:xy=3,
B、根據反比例函數系數k的幾何意義,陰影部分面積和為:3,
C、根據反比例函數系數k的幾何意義,以及梯形面積求法可得出:
陰影部分面積為:3+![]() ×(1+3)×2﹣
×(1+3)×2﹣![]() ﹣
﹣![]() =4,
=4,
D、根據M,N點的坐標以及三角形面積求法得出,陰影部分面積為:![]() ×1×6=3,
×1×6=3,
陰影部分面積最大的是4.
故選:C.
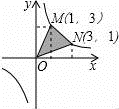
【點評】此題主要考查了反比例函數系數k的幾何意義以及三角形面積求法等知識,將圖形正確分割得出陰影部分面積是解題關鍵.
二、填空題(本題8小題,每小題4分,共計32分)
11.H7N9禽流感病毒的直徑大約為0.0000000805米,用科學記數法表示為 8.1×10﹣8 米(保留兩位有效數字)
【考點】科學記數法與有效數字.
【分析】首先利用科學記數法表示,再保留有效數字,有效數字的計算方法是:從左邊第一個不是0的數字起,后面所有的數字都是有效數字.用科學記數法表示的數的有效數字只與前面的a有關,與10的多少次方無關.
【解答】解:0.000 0000 805=8.05×10﹣8≈8.1×10﹣8,
故答案為:8.1×10﹣8.
【點評】此題主要考查科學記數法的表示方法,以及用科學記數法表示的數的有效數字的確定方法.
12.因式分解:4x3﹣36x= 4x(x+3)(x﹣3) .
【考點】提公因式法與公式法的綜合運用.
【分析】首先提公因式4x,然后利用平方差公式即可分解.
【解答】解:原式=4x(x2﹣9)=4x(x+3)(x﹣3).
故答案為:4x(x+3)(x﹣3).
【點評】本題考查了用提公因式法和公式法進行因式分解,一個多項式有公因式首先提取公因式,然后再用其他方法進行因式分解,同時因式分解要徹底,直到不能分解為止.
13.如圖,添加一個條件: ∠ADE=∠ACB ,使△ADE∽△ACB,(寫出一個即可)

【考點】相似三角形的判定.
【專題】開放型.
【分析】相似三角形的判定有三種方法:
①三邊法:三組對應邊的比相等的兩個三角形相似;
②兩邊及其夾角法:兩組對應邊的比相等且夾角對應相等的兩個三角形相似;
③兩角法:有兩組角對應相等的兩個三角形相似.
由此可得出可添加的條件.
【解答】解:由題意得,∠A=∠A(公共角),
則可添加:∠ADE=∠ACB,利用兩角法可判定△ADE∽△ACB.
故答案可為:∠ADE=∠ACB(答案不唯一).
【點評】本題考查了相似三角形的判定,解答本題的關鍵是熟練掌握三角形相似的三種判定方法,本題答案不唯一.
14.在六盤水市組織的“五城聯創”演講比賽中,小明等25人進入總決賽,賽制規定,13人早上參賽,12人下午參賽,小明抽到上午比賽的概率是 ![]() .
.
【考點】概率公式.
【分析】一共有25人參加比賽,其中13人早上參賽,利用概率公式即可求出小明抽到上午比賽的概率.
【解答】解:∵在六盤水市組織的“五城聯創”演講比賽中,小明等25人進入總決賽,
又∵賽制規定,13人早上參賽,12人下午參賽,
∴小明抽到上午比賽的概率是:![]() .
.
故答案為:![]() .
.
【點評】此題考查了概率公式的應用.注意概率=所求情況數與總情況數之比.
15.如圖,梯形ABCD中,AD∥BC,AD=4,AB=5,BC=10,CD的垂直平分線交BC于E,連接DE,則四邊形ABED的周長等于 19 .
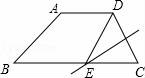
【考點】梯形;線段垂直平分線的性質.
【分析】根據線段垂直平分線上的點到線段兩端點的距離相等可得DE=CE,然后求出四邊形ABED的周長=AD+AB+BC,然后代入數據進行計算即可得解.
【解答】解:∵CD的垂直平分線交BC于E,
∴DE=CE,
∴四邊形ABED的周長=AD+AB+BE+DE=AD+AB+BC,
∵AD=4,AB=5,BC=10,
∴四邊形ABED的周長=4+5+10=19.
故答案為:19.
【點評】本題考查了梯形,線段垂直平分線上的點到線段兩端點的距離相等的性質,熟記線段垂直平分線的性質是解題的關鍵.
16.若⊙A和⊙B相切,它們的半徑分別為8cm和2cm,則圓心距AB為 10或6 cm.
【考點】圓與圓的位置關系.
【專題】分類討論.
【分析】本題應分內切和外切兩種情況討論.
【解答】解:∵⊙A和⊙B相切,
∴①當外切時,圓心距AB=8+2=10cm,
②當內切時,圓心距AB=8﹣2=6cm.
故答案為:10或6.
【點評】本題考查了由兩圓位置關系來判斷半徑和圓心距之間數量關系的方法.
外切時P=R+r;內切時P=R﹣r;注意分情況討論.
17.無論x取任何實數,代數式![]() 都有意義,則m的取值范圍為 m≥9 .
都有意義,則m的取值范圍為 m≥9 .
【考點】二次根式有意義的條件;非負數的性質:偶次方;配方法的應用.
【專題】壓軸題.
【分析】二次根式的被開方數是非負數,即x2﹣6x+m=(x﹣3)2﹣9+m≥0,所以(x﹣3)2≥9﹣m.通過偶次方(x﹣3)2是非負數可求得9﹣m≤0,則易求m的取值范圍.
【解答】解:由題意,得
x2﹣6x+m≥0,即(x﹣3)2﹣9+m≥0,
∵(x﹣3)2≥0,要使得(x﹣3)2﹣9+m恒大于等于0,
∴m﹣9≥0,
∴m≥9,
故答案為:m≥9.
【點評】考查了二次根式的意義和性質.概念:式子![]() (a≥0)叫二次根式.性質:二次根式中的被開方數必須是非負數,否則二次根式無意義.
(a≥0)叫二次根式.性質:二次根式中的被開方數必須是非負數,否則二次根式無意義.
18.把邊長為1的正方形紙片OABC放在直線m上,OA邊在直線m上,然后將正方形紙片繞著頂點A按順時針方向旋轉90°,此時,點O運動到了點O1處(即點B處),點C運動到了點C1處,點B運動到了點B1處,又將正方形紙片AO1C1B1繞B1點,按順時針方向旋轉90°…,按上述方法經過4次旋轉后,頂點O經過的總路程為 ![]() ,經過61次旋轉后,頂點O經過的總路程為
,經過61次旋轉后,頂點O經過的總路程為 ![]() .
.
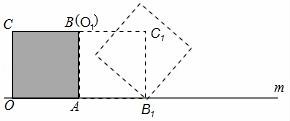
【考點】弧長的計算;正方形的性質;旋轉的性質.
【專題】壓軸題.
【分析】為了便于標注字母,且更清晰的觀察,每次旋轉后向右稍微平移一點,作出前幾次旋轉后的圖形,點O的第1次旋轉路線是以正方形的邊長為半徑,以90°圓心角的扇形,第2次旋轉路線是以正方形的對角線長為半徑,以90°圓心角的扇形,第3次旋轉路線是以正方形的邊長為半徑,以90°圓心角的扇形;
①根據弧長公式列式進行計算即可得解;
②求出61次旋轉中有幾個4次,然后根據以上的結論進行計算即可求解.
【解答】解:如圖,為了便于標注字母,且位置更清晰,每次旋轉后不防向右移動一點,
第1次旋轉路線是以正方形的邊長為半徑,以90°圓心角的扇形,路線長為![]() =
=![]() ;
;
第2次旋轉路線是以正方形的對角線長![]() 為半徑,以90°圓心角的扇形,路線長為
為半徑,以90°圓心角的扇形,路線長為![]() =
=![]() ;
;
第3次旋轉路線是以正方形的邊長為半徑,以90°圓心角的扇形,路線長為![]() =
=![]() ;
;
第4次旋轉點O沒有移動,旋轉后與最初正方形的放置相同,
因此4次旋轉,頂點O經過的路線長為![]() +
+![]() +
+![]() =
=![]() ;
;
∵61÷4=15…1,
∴經過61次旋轉,頂點O經過的路程是4次旋轉路程的15倍加上第1次路線長,即![]() ×15+
×15+![]() =
=![]() .
.
故答案為:![]() ;
;![]() .
.
【點評】本題考查了旋轉變換的性質,正方形的性質以及弧長的計算,讀懂題意,并根據題意作出圖形更形象直觀,且有利于旋轉變換規律的發現.
三、解答題(本題共7個小題,共88分,解答時應寫出必要的文字說明,證明過程或演算步驟)
19.(1)![]() +(2013﹣π)0
+(2013﹣π)0
(2)先化簡,再求值:(![]() )
)![]() ,其中x2﹣4=0.
,其中x2﹣4=0.
【考點】分式的化簡求值;實數的運算;零指數冪;負整數指數冪.
【專題】計算題.
【分析】(1)分別根據0指數冪、負整數指數冪的計算法則及絕對值的性質、特殊角的三角函數值計算出各數,再根據實數混合運算的法則進行計算即可;
(2)先根據分式混合運算的法則把原式進行化簡,再根據x2﹣4=0求出x的值代入進行計算即可.
【解答】解:(1)原式=3![]() ﹣9+2﹣
﹣9+2﹣![]() ﹣2×
﹣2×![]() +1
+1
=3![]() ﹣7﹣3
﹣7﹣3![]() +1=﹣6;
+1=﹣6;
(2)原式=(![]() +
+![]() )÷
)÷![]()
=![]() ×
×![]()
=![]() ×
×![]()
=![]() ,
,
∵x2﹣4=0,
∴x1=2(舍去),x2=﹣2,
∴原式=![]() =1.
=1.
【點評】本題考查的是分式的化簡求值及實數的運算,在解(2)時要注意x的取值要保證分式有意義.
20.為了了解中學生參加體育活動的情況,某校對部分學生進行了調查,其中一個問題是:“你平均每天參加體育活動的時間是多少?”共有4個選項:
A.1.5小時以上??? B.1﹣﹣1.5小時??? C.0.5小時?? D.0.5小時以下
根據調查結果繪制了兩幅不完整的統計圖.
請你根據以上信息解答下列問題:
(1)本次調查活動采取了 抽樣 調查方式.
(2)計算本次調查的學生人數和圖(2)選項C的圓心角度數.
(3)請根據圖(1)中選項B的部分補充完整.
(4)若該校有3000名學生,你估計該校可能有多少名學生平均每天參加體育活動的時間在0.5小時以下.
【考點】條形統計圖;用樣本估計總體;扇形統計圖.
【分析】(1)根據題意可得這次調查是抽樣調查;
(2)利用選A的人數÷選A的人數所占百分比即可算出總數;再利用360°×選C的人數所占百分比即可得到圓心角度數;
(3)用總數減去選A、C、D的人數即可得到選B的人數,再補全圖形即可;
(4)根據樣本估計總體的方法計算即可.
【解答】解:(1)抽樣調查;
(2)本次調查的學生人數:60÷30%=200(人),
選項C的圓心角度數:360°×![]() =54°;
=54°;
(3)選B的人數:200﹣60﹣30﹣10=100(人),如圖所示:
(4)3000×5%=150(人),
答:該校可能有150名學生平均每天參加體育活動的時間在0.5小時以下.
【點評】此題主要考查了條形統計圖和扇形統計圖的綜合運用,讀懂統計圖,從不同的統計圖中得到必要的信息是解決問題的關鍵.條形統計圖能清楚地表示出每個項目的數據;扇形統計圖直接反映部分占總體的百分比大小.
21.在Rt△ACB中,∠C=90°,點O在AB上,以O為圓心,OA長為半徑的圓與AC,AB分別交于點D,E,且∠CBD=∠A.
(1)判斷直線BD與⊙O的位置關系,并證明你的結論.
(2)若AD:AO=6:5,BC=3,求BD的長.

【考點】切線的判定.
【分析】(1)連接OD,DE,求出∠ADE=90°=∠C推出DE∥BC,∴∠EDB=∠CBD=∠A,根據∠A+∠OED=90°,求出∠EDB+∠ODE=90°,根據切線的判定推出即可;??
(2)求出AD:AE:DE=6:10:8,求出△ADE∽△BCD,推出AD:AE:DE=BC:BD:CD=6:10:8,代入求出即可.
【解答】(1)直線BD與⊙O的位置關系是相切,
證明:連接OD,DE,
∵∠C=90°,
∴∠CBD+∠CDB=90°,
∵∠A=∠CBD,
∴∠A+∠CDB=90°,
∵OD=OA,
∴∠A=∠ADO,
∴∠ADO+∠CDB=90°,
∴∠ODB=180°﹣90°=90°,
∴OD⊥BD,
∵OD為半徑,
∴BD是⊙O切線;
(2)解:∵AD:AO=6:5,
∴AD:AE=6:10,
∴AD:AE:DE=6:10:8,
∵AE是直徑,
∴∠ADE=∠C=90°,
∵∠CBD=∠A,
∴△ADE∽△BCD,
∴AD:AE:DE=BC:BD:CD=6:10:8,
即BC:BD=6:10,
∵BC=3,
∴BD=5.
【點評】本題考查了切線的判定,平行線性質和判定,等腰三角形性質和判定,相似三角形的性質和判定的應用,主要考查學生的推理能力.
22.閱讀材料:
關于三角函數還有如下的公式:
sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)=![]()
利用這些公式可以將一些不是特殊角的三角函數轉化為特殊角的三角函數來求值.
例:tan15°=tan(45°﹣30°)=![]() =
= =
=![]()
根據以上閱讀材料,請選擇適當的公式解答下面問題
(1)計算:sin15°;
(2)烏蒙鐵塔是六盤水市標志性建筑物之一(圖1),小華想用所學知識來測量該鐵塔的高度,如圖2,小華站在離塔底A距離7米的C處,測得塔頂的仰角為75°,小華的眼睛離地面的距離DC為1.62米,請幫助小華求出烏蒙鐵塔的高度.(精確到0.1米,參考數據![]() ,
,![]() )
)

【考點】解直角三角形的應用-仰角俯角問題.
【分析】(1)把15°化為45°﹣30°以后,再利用公式sin(α±β)=sinαcosβ![]() cosasinβ計算,即可求出sin15°的值;
cosasinβ計算,即可求出sin15°的值;
(2)先根據銳角三角函數的定義求出BE的長,再根據AB=AE+BE即可得出結論.
【解答】解:(1)sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°=![]() ×
×![]() ﹣
﹣![]() ×
×![]() =
=![]() ﹣
﹣![]() =
=![]() ;
;
(2)在Rt△BDE中,∵∠BED=90°,∠BDE=75°,DE=AC=7米,
∴BE=DE?tan∠BDE=DE?tan75°.
∵tan75°=tan(45°+30°)=![]() =
=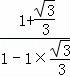 =2+
=2+![]() ,
,
∴BE=7(2+![]() )=14+7
)=14+7![]() ,
,
∴AB=AE+BE=1.62+14+7![]() ≈27.7(米).
≈27.7(米).
答:烏蒙鐵塔的高度約為27.7米.
【點評】本題考查了:
(1)特殊角的三角函數值的應用,屬于新題型,解題的關鍵是根據題目中所給信息結合特殊角的三角函數值來求解.
(2)解直角三角形的應用﹣仰角俯角問題,先根據銳角三角函數的定義得出BE的長是解題的關鍵.
23.為了抓住2013年涼都消夏文化節的商機,某商場決定購進甲、乙兩種紀念品,若購進甲種紀念品1件,乙種紀念品2件,需要160元;購進甲種紀念品2件,乙種紀念品3件,需要280元.
(1)購進甲乙兩種紀念品每件各需要多少元?
(2)該商場決定購進甲乙兩種紀念品100件,并且考慮市場需求和資金周轉,用于購買這些紀念品的資金不少于6000元,同時又不能超過6430元,則該商場共有幾種進貨方案?
(3)若銷售每件甲種紀念品可獲利30元,每件乙種紀念品可獲利12元,在第(2)問中的各種進貨方案中,哪種方案獲利最大?最大利潤是多少元?
【考點】一元一次不等式組的應用;二元一次方程組的應用.
【分析】(1)設購進甲乙兩種紀念品每件各需要x元和y元,根據購進甲種紀念品1件,乙種紀念品2件,需要160元;購進甲種紀念品2件,乙種紀念品3件,需要280元列出方程,求出x,y的值即可;
(2)設購進甲種紀念品a件,則乙種紀念品(100﹣a)件,根據購進甲乙兩種紀念品100件和購買這些紀念品的資金不少于6000元,同時又不能超過6430元列出不等式組,求出a的取值范圍,再根據a只能取整數,得出進貨方案;
(3)根據實際情況計算出各種方案的利潤,比較即可.
【解答】解:(1)設購進甲乙兩種紀念品每件各需要x元和y元,根據題意得:
![]() ,
,
解得:![]() ,
,
答:購進甲乙兩種紀念品每件各需要80元和40元;
(2)設購進甲種紀念品a件,則乙種紀念品(100﹣a)件,根據題意得:
![]() ,
,
解得:50≤a≤![]() ,
,
∵a只能取整數,a=50,51,52,53,54,55,56,57,58,59,60,
∴共11種進貨方案,
方案1:購進甲種紀念品50件,則購進乙種紀念品50件;
方案2:購進甲種紀念品51件,則購進乙種紀念品49件;
方案3:購進甲種紀念品52件,則購進乙種紀念品48件;
方案4:購進甲種紀念品53件,則購進乙種紀念品47件;
方案5:購進甲種紀念品54件,則購進乙種紀念品46件;
方案6:購進甲種紀念品55件,則購進乙種紀念品45件;
方案7:購進甲種紀念品56件,則購進乙種紀念品44件;
方案8:購進甲種紀念品57件,則購進乙種紀念品43件;
方案9:購進甲種紀念品58件,則購進乙種紀念品42件;
方案10:購進甲種紀念品59件,則購進乙種紀念品41件;
方案11:購進甲種紀念品60件,則購進乙種紀念品40件;
(3)因為甲種紀念品獲利最高,
所以甲種紀念品的數量越多總利潤越高,
因此選擇購進甲種紀念品60件,購進乙種紀念品40件利潤最高,
總利潤=60×30+40×12=2280(元)
則購進甲種紀念品60件,購進乙種紀念品40件時,可獲最大利潤,最大利潤是2280元.
【點評】此題考查了一元一次不等式組的應用和二元一次方程組的應用,讀懂題意,找到相應的關系,列出式子是解題的關鍵,注意第二問應求得整數解.
24.(1)觀察發現
?? 如圖(1):若點A、B在直線m同側,在直線m上找一點P,使AP+BP的值最小,做法如下:
?? 作點B關于直線m的對稱點B′,連接AB′,與直線m的交點就是所求的點P,線段AB′的長度即為AP+BP的最小值.
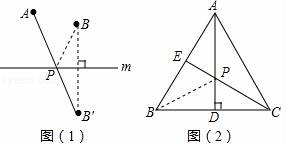
?? 如圖(2):在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小,做法如下:
作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這點就是所求的點P,故BP+PE的最小值為 ![]() .
.
(2)實踐運用
?? 如圖(3):已知⊙O的直徑CD為2,![]() 的度數為60°,點B是
的度數為60°,點B是![]() 的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的最小值為
的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的最小值為 ![]() .
.
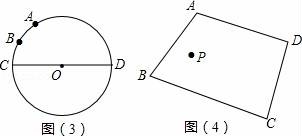
? (3)拓展延伸
如圖(4):點P是四邊形ABCD內一點,分別在邊AB、BC上作出點M,點N,使PM+PN+MN的值最小,保留作圖痕跡,不寫作法.
【考點】圓的綜合題;軸對稱-最短路線問題.
【專題】壓軸題.
【分析】(1)觀察發現:利用作法得到CE的長為BP+PE的最小值;由AB=2,點E是AB的中點,根據等邊三角形的性質得到CE⊥AB,∠BCE=![]() ∠BCA=30°,BE=1,再根據含30度的直角三角形三邊的關系得CE=
∠BCA=30°,BE=1,再根據含30度的直角三角形三邊的關系得CE=![]() ;
;
(2)實踐運用:過B點作弦BE⊥CD,連結AE交CD于P點,連結OB、OE、OA、PB,根據垂徑定理得到CD平分BE,即點E與點B關于CD對稱,則AE的長就是BP+AP的最小值;
由于![]() 的度數為60°,點B是
的度數為60°,點B是![]() 的中點得到∠BOC=30°,∠AOC=60°,所以∠AOE=60°+30°=90°,于是可判斷△OAE為等腰直角三角形,則AE=
的中點得到∠BOC=30°,∠AOC=60°,所以∠AOE=60°+30°=90°,于是可判斷△OAE為等腰直角三角形,則AE=![]() OA=
OA=![]() ;
;
(3)拓展延伸:分別作出點P關于AB和BC的對稱點E和F,然后連結EF,EF交AB于M、交BC于N.
【解答】解:(1)觀察發現
如圖(2),CE的長為BP+PE的最小值,
∵在等邊三角形ABC中,AB=2,點E是AB的中點
∴CE⊥AB,∠BCE=![]() ∠BCA=30°,BE=1,
∠BCA=30°,BE=1,
∴CE=![]() BE=
BE=![]() ;
;
故答案為:![]() ;
;
(2)實踐運用
如圖(3),過B點作弦BE⊥CD,連結AE交CD于P點,連結OB、OE、OA、PB,
∵BE⊥CD,
∴CD平分BE,即點E與點B關于CD對稱,
∵![]() 的度數為60°,點B是
的度數為60°,點B是![]() 的中點,
的中點,
∴∠BOC=30°,∠AOC=60°,
∴∠EOC=30°,
∴∠AOE=60°+30°=90°,
∵OA=OE=1,
∴AE=![]() OA=
OA=![]() ,
,
∵AE的長就是BP+AP的最小值.
故答案為:![]() ;
;
(3)拓展延伸
作法:1、作點P關于直線AB的對稱點E,
2、作點P關于直線BC的對稱點F,
3、連接EF交AB于M,交BC于N,
則PM+PN+MN的值最小;
如圖(4)
【點評】本題考查了圓的綜合題:弧、弦和圓心角之間的關系以及圓周角定理在有關圓的幾何證明中經常用到,同時熟練掌握等邊三角形的性質以及軸對稱﹣最短路徑問題.
25.已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=![]() ,若以O為坐標原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.
,若以O為坐標原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.
(1)求經過點O,C,A三點的拋物線的解析式.
(2)求拋物線的對稱軸與線段OB交點D的坐標.
(3)線段OB與拋物線交于點E,點P為線段OE上一動點(點P不與點O,點E重合),過P點作y軸的平行線,交拋物線于點M,問:在線段OE上是否存在這樣的點P,使得PD=CM?若存在,請求出此時點P的坐標;若不存在,請說明理由.
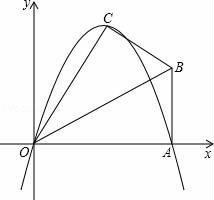
【考點】二次函數綜合題.
【專題】壓軸題.
【分析】(1)在Rt△AOB中,根據AO的長和∠BOA的度數,可求得OB的長,根據折疊的性質即可得到OA=OC,且∠BOC=∠BOA=30°,過C作CD⊥x軸于D,即可根據∠COD的度數和OC的長求得CD、OD的值,從而求出點C、A的坐標,將A、C、O的坐標代入拋物線的解析式中,通過聯立方程組即可求出待定系數的值,從而確定該拋物線的解析式.
(2)求出直線BO的解析式,進而利用x=![]() 求出y的值,即可得出D點坐標;
求出y的值,即可得出D點坐標;
(3)根據(1)所得拋物線的解析式可得到其頂點的坐標(即C點),設直線MP與x軸的交點為N,且PN=t,在Rt△OPN中,根據∠PON的度數,易得PN、ON的長,即可得到點P的坐標,然后根據點P的橫坐標和拋物線的解析式可求得M點的縱坐標,過M作MF⊥CD(即拋物線對稱軸)于F,過P作PQ⊥CD于Q,若PD=CM,那么CF=QD,根據C、M、P、D四點縱坐標,易求得CF、QD的長,聯立兩式即可求出此時t的值,從而求得點P的坐標.
【解答】解:(1)過點C作CH⊥x軸,垂足為H;
∵在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=![]() ,
,
∴OB=![]() =4,AB=2;
=4,AB=2;
由折疊的性質知:∠COB=30°,OC=AO=2![]() ,
,
∴∠COH=60°,OH=![]() ,CH=3;
,CH=3;
∴C點坐標為(![]() ,3).
,3).
∵O點坐標為:(0,0),
∴拋物線解析式為y=ax2+bx(a≠0),
∵圖象經過C(![]() ,3)、A(2
,3)、A(2![]() ,0)兩點,
,0)兩點,
∴![]() ,
,
解得![]() ;
;
∴此拋物線的函數關系式為:y=﹣x2+2![]() x.
x.
(2)∵AO=2![]() ,AB=2,
,AB=2,
∴B點坐標為:(2![]() ,2),
,2),
∴設直線BO的解析式為:y=kx,
則2=2![]() k,
k,
解得:k=![]() ,
,
∴y=![]() x,
x,
∵y=﹣x2+2![]() x的對稱軸為直線x=﹣
x的對稱軸為直線x=﹣![]() =﹣
=﹣![]() =
=![]() ,
,
∴將兩函數聯立得出:y=![]() ×
×![]() =1,
=1,
∴拋物線的對稱軸與線段OB交點D的坐標為:(![]() ,1);
,1);
(3)存在.
∵y=﹣x2+2![]() x的頂點坐標為(
x的頂點坐標為(![]() ,3),
,3),
即為點C,MP⊥x軸,垂足為N,設PN=t;
∵∠BOA=30°,
∴ON=![]() t,
t,
∴P(![]() t,t);
t,t);
作PQ⊥CD,垂足為Q,MF⊥CD,垂足為F;
把x=![]() t代入y=﹣x2+2
t代入y=﹣x2+2![]() x,
x,
得y=﹣3t2+6t,
∴M(![]() t,﹣3t2+6t),F(
t,﹣3t2+6t),F(![]() ,﹣3t2+6t),
,﹣3t2+6t),
同理:Q(![]() ,t),D(
,t),D(![]() ,1);
,1);
要使PD=CM,只需CF=QD,
即3﹣(﹣3t2+6t)=|t﹣1|,
解得t=![]() ,t=1(不合題意舍去),t=
,t=1(不合題意舍去),t=![]() ,
,
∴P點坐標為(![]()
![]() ,
,![]() ),或(
),或(![]() ,
,![]() ),
),
∴存在滿足條件的P點,使得PD=CM,此時P點坐標為(![]()
![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
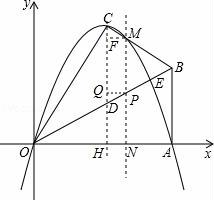
【點評】此題主要考查了圖形的旋轉變化、解直角三角形、二次函數解析式的確定等重要知識點,表示出P點坐標利用CF=QD求出是解題關鍵.
第8頁(共29頁)

孔乙己是貧困潦倒的知識分子。在書中,孔乙己是一個知識分子,滿口“之乎者也”,但是他很窮,還竊書,說過“讀書人的事,怎么能叫竊,”被人嘲笑,他...

自然界產生氧氣的化學方程式:光合作用的反應式為6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反應和暗反應兩個過程。需要具備光...

有的高校沒有條件,只要學業水平成績都合格就可以,比如中國科學院大學。有的需要平常學習考試成績,比如北京外國語大學要求高三第一學期期末成績在全...

在四則運算中,表示計算順序,在小括號之后、大括號之前;表示兩個整數的最小公倍數;表示取未知數的整數部分;在函數中,表示函數的閉區間;在線性代...

濟南開設的最好的職高學校有:濟南方信集團職業高中、濟南公共交通職業高中。濟南市公共交通職業高級中學是由濟南市公共交通總公司承辦,業務屬濟南市...

實然:是說事物實際上就是這樣的,但不同于現實性(現實性指其有合理性和客觀性);應然:就是應該是怎么樣的意思,比如說這件事,就應該是那樣的結果...

地中海氣候一種夏季炎熱干燥、冬季溫和多雨,雨熱不同期的氣候類型。地中海氣候冬季受西風帶控制,鋒面氣旋頻繁活動,氣候溫和,最冷月的氣溫在4-1...

堿石灰,又稱鈉石灰,堿石灰是白色或米黃色粉末,疏松多孔,是氧化鈣(CaO,大約75%),水(H?O,大約20%),氫氧化鈉(NaOH,大約3...