2017年江西省新余中考數(shù)學(xué)試題（word版 含答案）

為了方便您的閱讀請點擊全屏查看

一、選擇題（本大題共6個小題，每小題3分，共18分.在每小題給出的四個選項中，只有一項是符合題目要求的.）

1．﹣6的相反數(shù)是（）

A．????????????? B．﹣????????????? C．6????????????? D．﹣6

2．在國家“一帶一路”戰(zhàn)略下，我國與歐洲開通了互利互惠的中歐班列．行程最長，途經(jīng)城市和國家最多的一趟專列全程長13000km，將13000用科學(xué)記數(shù)法表示應(yīng)為（）

A．0.13×105????????????? B．1.3×104????????????? C．1.3×105????????????? D．13×103

3．下列圖形中，是軸對稱圖形的是（）

A．????????????? B．????????????? C．????????????? D．

4．下列運算正確的是（）

A．（﹣a5）2=a10????????????? B．2a?3a2=6a2

C．﹣2a+a=﹣3a????????????? D．﹣6a6÷2a2=﹣3a3

5．已知一元二次方程2x2﹣5x+1=0的兩個根為x1，x2，下列結(jié)論正確的是（）

A．x1+x2=﹣????????????? B．x1?x2=1

C．x1，x2都是有理數(shù)????????????? D．x1，x2都是正數(shù)

6．如圖，任意四邊形ABCD中，E，F(xiàn)，G，H分別是AB，BC，CD，DA上的點，對于四邊形EFGH的形狀，某班學(xué)生在一次數(shù)學(xué)活動課中，通過動手實踐，探索出如下結(jié)論，其中錯誤的是（）

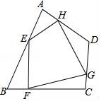
A．當(dāng)E，F(xiàn)，G，H是各邊中點，且AC=BD時，四邊形EFGH為菱形

B．當(dāng)E，F(xiàn)，G，H是各邊中點，且AC⊥BD時，四邊形EFGH為矩形

C．當(dāng)E，F(xiàn)，G，H不是各邊中點時，四邊形EFGH可以為平行四邊形

D．當(dāng)E，F(xiàn)，G，H不是各邊中點時，四邊形EFGH不可能為菱形

二、填空題（本大題共6小題，每小題3分，滿分18分，將答案填在答題紙上）

7．函數(shù)y=中，自變量x的取值范圍是　?? 　．

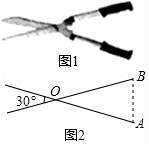
8．如圖1是一把園林剪刀，把它抽象為圖2，其中OA=OB．若剪刀張開的角為30°，則∠A=　?? 　度．

9．中國人最先使用負數(shù)，魏晉時期的數(shù)學(xué)家劉徽在“正負術(shù)”的注文中指出，可將算籌（小棍形狀的記數(shù)工具）正放表示正數(shù)，斜放表示負數(shù)．如圖，根據(jù)劉徽的這種表示法，觀察圖①，可推算圖②中所得的數(shù)值為　?? 　．

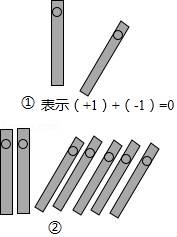
10．如圖，正三棱柱的底面周長為9，截去一個底面周長為3的正三棱柱，所得幾何體的俯視圖的周長是　?? 　．

11．已知一組從小到大排列的數(shù)據(jù)：2，5，x，y，2x，11的平均數(shù)與中位數(shù)都是7，則這組數(shù)據(jù)的眾數(shù)是　?? 　．

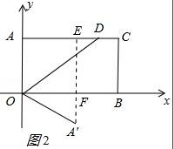
12．已知點A（0，4），B（7，0），C（7，4），連接AC，BC得到矩形AOBC，點D的邊AC上，將邊OA沿OD折疊，點A的對應(yīng)邊為A'．若點A'到矩形較長兩對邊的距離之比為1：3，則點A'的坐標(biāo)為　?? 　．

三、解答題（本大題共5小題，每小題6分，共30分.解答應(yīng)寫出文字說明、證明過程或演算步驟.）

13．（1）計算：÷；

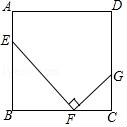
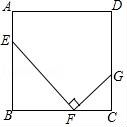
（2）如圖，正方形ABCD中，點E，F(xiàn)，G分別在AB，BC，CD上，且∠EFG=90°．求證：△EBF∽△FCG．

14．解不等式組：，并把解集在數(shù)軸上表示出來．

15．端午節(jié)那天，小賢回家看到桌上有一盤粽子，其中有豆沙粽、肉粽各1個，蜜棗粽2個，這些粽子除餡外無其他差別．

（1）小賢隨機地從盤中取出一個粽子，取出的是肉粽的概率是多少？

（2）小賢隨機地從盤中取出兩個粽子，試用畫樹狀圖或列表的方法表示所有可能的結(jié)果，并求出小賢取出的兩個都是蜜棗粽的概率．

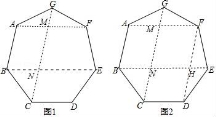
16．如圖，已知正七邊形ABCDEFG，請僅用無刻度的直尺，分別按下列要求畫圖．

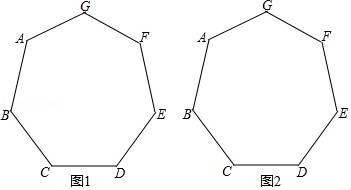
（1）在圖1中，畫出一個以AB為邊的平行四邊形；

（2）在圖2中，畫出一個以AF為邊的菱形．

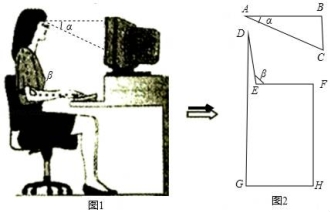
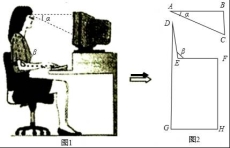
17．如圖1，研究發(fā)現(xiàn)，科學(xué)使用電腦時，望向熒光屏幕畫面的“視線角”α約為20°，而當(dāng)手指接觸鍵盤時，肘部形成的“手肘角”β約為100°．圖2是其側(cè)面簡化示意圖，其中視線AB水平，且與屏幕BC垂直．

（1）若屏幕上下寬BC=20cm，科學(xué)使用電腦時，求眼睛與屏幕的最短距離AB的長；

（2）若肩膀到水平地面的距離DG=100cm，上臂DE=30cm，下臂EF水平放置在鍵盤上，其到地面的距離FH=72cm．請判斷此時β是否符合科學(xué)要求的100°？

（參考數(shù)據(jù)：sin69°≈，cos21°≈，tan20°≈，tan43°≈，所有結(jié)果精確到個位）

四、（本大題共3小題，每小題8分，共24分）.

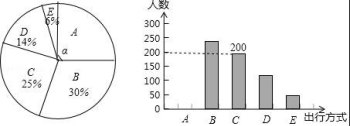
18．為了解某市市民“綠色出行”方式的情況，某校數(shù)學(xué)興趣小組以問卷調(diào)查的形式，隨機調(diào)查了某市部分出行市民的主要出行方式（參與問卷調(diào)查的市民都只從以下五個種類中選擇一類），并將調(diào)查結(jié)果繪制成如下不完整的統(tǒng)計圖．

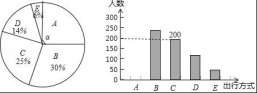
根據(jù)以上信息，回答下列問題：

（1）參與本次問卷調(diào)查的市民共有　?? 　人，其中選擇B類的人數(shù)有　?? 　人；

（2）在扇形統(tǒng)計圖中，求A類對應(yīng)扇形圓心角α的度數(shù)，并補全條形統(tǒng)計圖；

（3）該市約有12萬人出行，若將A，B，C這三類出行方式均視為“綠色出行”方式，請估計該市“綠色出行”方式的人數(shù)．

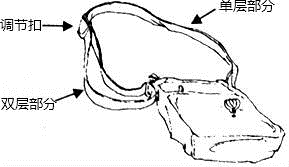
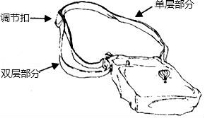
19．如圖，是一種斜挎包，其挎帶由雙層部分、單層部分和調(diào)節(jié)扣構(gòu)成．小敏用后發(fā)現(xiàn)，通過調(diào)節(jié)扣加長或縮短單層部分的長度，可以使挎帶的長度（單層部分與雙層部分長度的和，其中調(diào)節(jié)扣所占的長度忽略不計）加長或縮短．設(shè)單層部分的長度為xcm，雙層部分的長度為ycm，經(jīng)測量，得到如下數(shù)據(jù)：

（1）根據(jù)表中數(shù)據(jù)的規(guī)律，完成以下表格，并直接寫出y關(guān)于x的函數(shù)解析式；

（2）根據(jù)小敏的身高和習(xí)慣，挎帶的長度為120cm時，背起來正合適，請求出此時單層部分的長度；

（3）設(shè)挎帶的長度為lcm，求l的取值范圍．

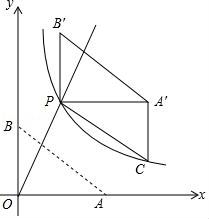
20．如圖，直線y=k1x（x≥0）與雙曲線y=（x＞0）相交于點P（2，4）．已知點A（4，0），B（0，3），連接AB，將Rt△AOB沿OP方向平移，使點O移動到點P，得到△A'PB'．過點A'作A'C∥y軸交雙曲線于點C．

（1）求k1與k2的值；

（2）求直線PC的表達式；

（3）直接寫出線段AB掃過的面積．

五、（本大題共2小題，每小題9分，共18分）.

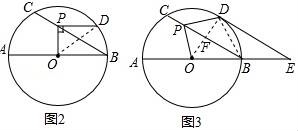
21．如圖1，⊙O的直徑AB=12，P是弦BC上一動點（與點B，C不重合），∠ABC=30°，過點P作PD⊥OP交⊙O于點D．

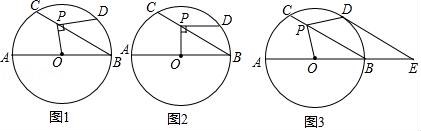
（1）如圖2，當(dāng)PD∥AB時，求PD的長；

（2）如圖3，當(dāng)=時，延長AB至點E，使BE=AB，連接DE．

①求證：DE是⊙O的切線；

②求PC的長．

22．已知拋物線C1：y=ax2﹣4ax﹣5（a＞0）．

（1）當(dāng)a=1時，求拋物線與x軸的交點坐標(biāo)及對稱軸；

（2）①試說明無論a為何值，拋物線C1一定經(jīng)過兩個定點，并求出這兩個定點的坐標(biāo)；

②將拋物線C1沿這兩個定點所在直線翻折，得到拋物線C2，直接寫出C2的表達式；

（3）若（2）中拋物線C2的頂點到x軸的距離為2，求a的值．

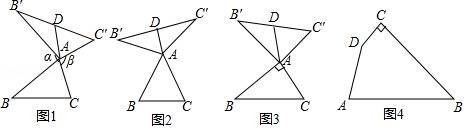
六、（本大題共12分）

23．我們定義：如圖1，在△ABC看，把AB點繞點A順時針旋轉(zhuǎn)α（0°＜α＜180°）得到AB'，把AC繞點A逆時針旋轉(zhuǎn)β得到AC'，連接B'C'．當(dāng)α+β=180°時，我們稱△A'B'C'是△ABC的“旋補三角形”，△AB'C'邊B'C'上的中線AD叫做△ABC的“旋補中線”，點A叫做“旋補中心”．

特例感知：

（1）在圖2，圖3中，△AB'C'是△ABC的“旋補三角形”，AD是△ABC的“旋補中線”．

①如圖2，當(dāng)△ABC為等邊三角形時，AD與BC的數(shù)量關(guān)系為AD=　?? 　BC；

②如圖3，當(dāng)∠BAC=90°，BC=8時，則AD長為　?? 　．

猜想論證：

（2）在圖1中，當(dāng)△ABC為任意三角形時，猜想AD與BC的數(shù)量關(guān)系，并給予證明．

拓展應(yīng)用

（3）如圖4，在四邊形ABCD，∠C=90°，∠D=150°，BC=12，CD=2，DA=6．在四邊形內(nèi)部是否存在點P，使△PDC是△PAB的“旋補三角形”？若存在，給予證明，并求△PAB的“旋補中線”長；若不存在，說明理由．

2017年江西省新余中考數(shù)學(xué)試題參考答案與試題解析

　一、選擇題（本大題共6個小題，每小題3分，共18分.在每小題給出的四個選項中，只有一項是符合題目要求的.）

1．﹣6的相反數(shù)是（）

A．????????????? B．﹣????????????? C．6????????????? D．﹣6

【考點】14：相反數(shù)．

【分析】求一個數(shù)的相反數(shù)，即在這個數(shù)的前面加負號．

【解答】解：﹣6的相反數(shù)是6，

故選C

2．在國家“一帶一路”戰(zhàn)略下，我國與歐洲開通了互利互惠的中歐班列．行程最長，途經(jīng)城市和國家最多的一趟專列全程長13000km，將13000用科學(xué)記數(shù)法表示應(yīng)為（）

A．0.13×105????????????? B．1.3×104????????????? C．1.3×105????????????? D．13×103

【考點】1I：科學(xué)記數(shù)法—表示較大的數(shù)．

【分析】科學(xué)記數(shù)法的表示形式為a×10n的形式，其中1≤|a|＜10，n為整數(shù)．確定n的值時，要看把原數(shù)變成a時，小數(shù)點移動了多少位，n的絕對值與小數(shù)點移動的位數(shù)相同．當(dāng)原數(shù)絕對值＞1時，n是正數(shù)；當(dāng)原數(shù)的絕對值＜1時，n是負數(shù)．

【解答】解：將13000用科學(xué)記數(shù)法表示為：1.3×104．

故選B．

3．下列圖形中，是軸對稱圖形的是（）

A．????????????? B．????????????? C．????????????? D．

【考點】P3：軸對稱圖形．

【分析】根據(jù)軸對稱圖形的概念求解．

【解答】解：A、不是軸對稱圖形，故A不符合題意；

B、不是軸對稱圖形，故B不符合題意；

C、是軸對稱圖形，故C符合題意；

D、不是軸對稱圖形，故D不符合題意；

故選：C．

4．下列運算正確的是（）

A．（﹣a5）2=a10????????????? B．2a?3a2=6a2

C．﹣2a+a=﹣3a????????????? D．﹣6a6÷2a2=﹣3a3

【考點】4I：整式的混合運算．

【分析】根據(jù)整式的運算法則即可求出答案．

【解答】解：（B）原式=6a3，故B錯誤；

（C）原式=a，故C錯誤；

（D）原式=﹣3a4，故D錯誤；

故選（A）

5．已知一元二次方程2x2﹣5x+1=0的兩個根為x1，x2，下列結(jié)論正確的是（）

A．x1+x2=﹣????????????? B．x1?x2=1

C．x1，x2都是有理數(shù)????????????? D．x1，x2都是正數(shù)

【考點】AB：根與系數(shù)的關(guān)系．

【分析】先利用根與系數(shù)的關(guān)系得到x1+x2=＞0，x1x2=＞0，然后利用有理數(shù)的性質(zhì)可判定兩根的符合．

【解答】解：根據(jù)題意得x1+x2=＞0，x1x2=＞0，

所以x1＞0，x2＞0．

故選D．

6．如圖，任意四邊形ABCD中，E，F(xiàn)，G，H分別是AB，BC，CD，DA上的點，對于四邊形EFGH的形狀，某班學(xué)生在一次數(shù)學(xué)活動課中，通過動手實踐，探索出如下結(jié)論，其中錯誤的是（）

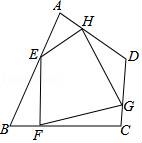
A．當(dāng)E，F(xiàn)，G，H是各邊中點，且AC=BD時，四邊形EFGH為菱形

B．當(dāng)E，F(xiàn)，G，H是各邊中點，且AC⊥BD時，四邊形EFGH為矩形

C．當(dāng)E，F(xiàn)，G，H不是各邊中點時，四邊形EFGH可以為平行四邊形

D．當(dāng)E，F(xiàn)，G，H不是各邊中點時，四邊形EFGH不可能為菱形

【考點】LN：中點四邊形．

【分析】連接四邊形各邊中點所得的四邊形必為平行四邊形，根據(jù)中點四邊形的性質(zhì)進行判斷即可．

【解答】解：A．當(dāng)E，F(xiàn)，G，H是各邊中點，且AC=BD時，EF=FG=GH=HE，故四邊形EFGH為菱形，故A正確；

B．當(dāng)E，F(xiàn)，G，H是各邊中點，且AC⊥BD時，∠EFG=∠FGH=∠GHE=90°，故四邊形EFGH為矩形，故B正確；

C．當(dāng)E，F(xiàn)，G，H不是各邊中點時，EF∥HG，EF=HG，故四邊形EFGH為平行四邊形，故C正確；

D．當(dāng)E，F(xiàn)，G，H不是各邊中點時，四邊形EFGH可能為菱形，故D錯誤；

故選：D．

二、填空題（本大題共6小題，每小題3分，滿分18分，將答案填在答題紙上）

7．函數(shù)y=中，自變量x的取值范圍是　x≥2　．

【考點】E4：函數(shù)自變量的取值范圍．

【分析】根據(jù)二次根式的性質(zhì)，被開方數(shù)大于等于0，就可以求解．

【解答】解：依題意，得x﹣2≥0，

解得：x≥2，

故答案為：x≥2．

8．如圖1是一把園林剪刀，把它抽象為圖2，其中OA=OB．若剪刀張開的角為30°，則∠A=　75　度．

【考點】KH：等腰三角形的性質(zhì)．

【分析】根據(jù)等腰三角形的性質(zhì)和三角形的內(nèi)角和即可得到結(jié)論．

【解答】解：∵OA=OB，∠AOB=30°，

∴∠A==75°，

故答案為：75．

9．中國人最先使用負數(shù)，魏晉時期的數(shù)學(xué)家劉徽在“正負術(shù)”的注文中指出，可將算籌（小棍形狀的記數(shù)工具）正放表示正數(shù)，斜放表示負數(shù)．如圖，根據(jù)劉徽的這種表示法，觀察圖①，可推算圖②中所得的數(shù)值為　﹣3　．

【考點】11：正數(shù)和負數(shù)．

【分析】根據(jù)有理數(shù)的加法，可得答案．

【解答】解：圖②中表示（+2）+（﹣5）=﹣3，

故答案為：﹣3．　

10．如圖，正三棱柱的底面周長為9，截去一個底面周長為3的正三棱柱，所得幾何體的俯視圖的周長是　8　．

【考點】U2：簡單組合體的三視圖；I9：截一個幾何體．

【分析】根據(jù)從上邊看得到的圖形是俯視圖，可得答案．

【解答】解：從上邊看是一個梯形：上底是1，下底是3，兩腰是2，

周長是1+2+2+3=8，

故答案為：8．

11．已知一組從小到大排列的數(shù)據(jù)：2，5，x，y，2x，11的平均數(shù)與中位數(shù)都是7，則這組數(shù)據(jù)的眾數(shù)是　5　．

【考點】W5：眾數(shù)；W1：算術(shù)平均數(shù)；W4：中位數(shù)．

【分析】根據(jù)平均數(shù)與中位數(shù)的定義可以先求出x，y的值，進而就可以確定這組數(shù)據(jù)的眾數(shù)即可．

【解答】解：∵一組從小到大排列的數(shù)據(jù)：2，5，x，y，2x，11的平均數(shù)與中位數(shù)都是7，

∴（2+5+x+y+2x+11）=（x+y）=7，

解得y=9，x=5，

∴這組數(shù)據(jù)的眾數(shù)是5．

故答案為5．

12．已知點A（0，4），B（7，0），C（7，4），連接AC，BC得到矩形AOBC，點D的邊AC上，將邊OA沿OD折疊，點A的對應(yīng)邊為A'．若點A'到矩形較長兩對邊的距離之比為1：3，則點A'的坐標(biāo)為　：（，3）或（，1）或（2，﹣2）　．

【考點】PB：翻折變換（折疊問題）；D5：坐標(biāo)與圖形性質(zhì)；LB：矩形的性質(zhì)．

【分析】由已知得出∠A=90°，BC=OA=4，OB=AC=7，分兩種情況：（1）當(dāng)點A'在矩形AOBC的內(nèi)部時，過A'作OB的垂線交OB于F，交AC于E，當(dāng)A'E：A'F=1：3時，求出A'E=1，A'F=3，由折疊的性質(zhì)得：OA'=OA=4，∠OA'D=∠A=90°，在Rt△OA'F中，由勾股定理求出OF==，即可得出答案；

②當(dāng)A'E：A'F=3：1時，同理得：A'（，1）；

（2）當(dāng)點A'在矩形AOBC的外部時，此時點A'在第四象限，過A'作OB的垂線交OB于F，交AC于E，由A'F：A'E=1：3，則A'F：EF=1：2，求出A'F=EF=BC=2，在Rt△OA'F中，由勾股定理求出OF=2，即可得出答案．

【解答】解：∵點A（0，4），B（7，0），C（7，4），

∴BC=OA=4，OB=AC=7，

分兩種情況：

（1）當(dāng)點A'在矩形AOBC的內(nèi)部時，過A'作OB的垂線交OB于F，交AC于E，如圖1所示：

①當(dāng)A'E：A'F=1：3時，

∵A'E+A'F=BC=4，

∴A'E=1，A'F=3，

由折疊的性質(zhì)得：OA'=OA=4，

在Rt△OA'F中，由勾股定理得：OF==，

∴A'（，3）；

②當(dāng)A'E：A'F=3：1時，同理得：A'（，1）；

（2）當(dāng)點A'在矩形AOBC的外部時，此時點A'在第四象限，過A'作OB的垂線交OB于F，交AC于E，如圖2所示：∵A'F：A'E=1：3，則A'F：EF=1：2，

∴A'F=EF=BC=2，

由折疊的性質(zhì)得：OA'=OA=4，

在Rt△OA'F中，由勾股定理得：OF==2，

∴A'（2，﹣2）；

故答案為：（，3）或（，1）或（2，﹣2）．

三、解答題（本大題共5小題，每小題6分，共30分.解答應(yīng)寫出文字說明、證明過程或演算步驟.）

13．（1）計算：÷；

（2）如圖，正方形ABCD中，點E，F(xiàn)，G分別在AB，BC，CD上，且∠EFG=90°．求證：△EBF∽△FCG．

【考點】S8：相似三角形的判定；6A：分式的乘除法；LE：正方形的性質(zhì)．

【分析】（1）先把分母因式分解，再把除法運算化為乘法運算，然后約分即可；

（2）先根據(jù)正方形的性質(zhì)得∠B=∠C=90°，再利用等角的余角相等得∠BEF=∠CFG，然后根據(jù)有兩組角對應(yīng)相等的兩個三角形相似可判定△EBF∽△FCG．

【解答】（1）解：原式=?

=；

（2）證明：∵四邊形ABCD為正方形，

∴∠B=∠C=90°，

∴∠BEF+∠BFE=90°，

∵∠EFG=90°，

∴∠BFE+∠CFG=90°，

∴∠BEF=∠CFG，

∴△EBF∽△FCG．

14．解不等式組：，并把解集在數(shù)軸上表示出來．

【考點】CB：解一元一次不等式組；C4：在數(shù)軸上表示不等式的解集．

【分析】分別求出每一個不等式的解集，根據(jù)解集在數(shù)軸上的表示即可確定不等式組的解集．

【解答】解：解不等式﹣2x＜6，得：x＞﹣3，

解不等式3（x﹣2）≤x﹣4，得：x≤1，

將不等式解集表示在數(shù)軸如下：

則不等式組的解集為﹣3＜x≤1　

15．端午節(jié)那天，小賢回家看到桌上有一盤粽子，其中有豆沙粽、肉粽各1個，蜜棗粽2個，這些粽子除餡外無其他差別．

（1）小賢隨機地從盤中取出一個粽子，取出的是肉粽的概率是多少？

（2）小賢隨機地從盤中取出兩個粽子，試用畫樹狀圖或列表的方法表示所有可能的結(jié)果，并求出小賢取出的兩個都是蜜棗粽的概率．

【考點】X6：列表法與樹狀圖法；X4：概率公式．

【分析】（1）直接利用概率公式求出取出的是肉粽的概率；

（2）直接列舉出所有的可能，進而利用概率公式求出答案．

【解答】解：（1）∵有豆沙粽、肉粽各1個，蜜棗粽2個，

∴隨機地從盤中取出一個粽子，取出的是肉粽的概率是：；

（2）如圖所示：

，

一共有12種可能，取出的兩個都是蜜棗粽的有2種，

故取出的兩個都是蜜棗粽的概率為： =．

16．如圖，已知正七邊形ABCDEFG，請僅用無刻度的直尺，分別按下列要求畫圖．

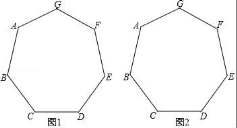
（1）在圖1中，畫出一個以AB為邊的平行四邊形；

（2）在圖2中，畫出一個以AF為邊的菱形．

【考點】N3：作圖—復(fù)雜作圖；L5：平行四邊形的性質(zhì)；L8：菱形的性質(zhì)．

【分析】（1）連接AF、BE、CG，CG交AF于M，交BE于N．四邊形ABNM是平行四邊形．

（2）連接AF、BE、CG，CG交AF于M，交BE于N，連接DF交BE于H，四邊形MNHF是菱形

【解答】解：（1）連接AF、BE、CG，CG交AF于M，交BE于N．四邊形ABNM是平行四邊形．

（2）連接AF、BE、CG，CG交AF于M，交BE于N，連接DF交BE于H，四邊形MNHF是菱形．

17．如圖1，研究發(fā)現(xiàn)，科學(xué)使用電腦時，望向熒光屏幕畫面的“視線角”α約為20°，而當(dāng)手指接觸鍵盤時，肘部形成的“手肘角”β約為100°．圖2是其側(cè)面簡化示意圖，其中視線AB水平，且與屏幕BC垂直．

（1）若屏幕上下寬BC=20cm，科學(xué)使用電腦時，求眼睛與屏幕的最短距離AB的長；

（2）若肩膀到水平地面的距離DG=100cm，上臂DE=30cm，下臂EF水平放置在鍵盤上，其到地面的距離FH=72cm．請判斷此時β是否符合科學(xué)要求的100°？

（參考數(shù)據(jù)：sin69°≈，cos21°≈，tan20°≈，tan43°≈，所有結(jié)果精確到個位）

【考點】T8：解直角三角形的應(yīng)用．

【分析】（1）Rt△ABC中利用三角函數(shù)即可直接求解；

（2）延長FE交DG于點I，利用三角函數(shù)求得∠DEI即可求得β的值，從而作出判斷．

【解答】解：（1）∵Rt△ABC中，tanA=，

∴AB====55（cm）；

（2）延長FE交DG于點I．

則DI=DG﹣FH=100﹣72=28（cm）．

在Rt△DEI中，sin∠DEI===，

∴∠DEI=69°，

∴∠β=180°﹣69°=111°≠100°，

∴此時β不是符合科學(xué)要求的100°．

四、（本大題共3小題，每小題8分，共24分）.

18．為了解某市市民“綠色出行”方式的情況，某校數(shù)學(xué)興趣小組以問卷調(diào)查的形式，隨機調(diào)查了某市部分出行市民的主要出行方式（參與問卷調(diào)查的市民都只從以下五個種類中選擇一類），并將調(diào)查結(jié)果繪制成如下不完整的統(tǒng)計圖．

根據(jù)以上信息，回答下列問題：

（1）參與本次問卷調(diào)查的市民共有　800　人，其中選擇B類的人數(shù)有　240　人；

（2）在扇形統(tǒng)計圖中，求A類對應(yīng)扇形圓心角α的度數(shù)，并補全條形統(tǒng)計圖；

（3）該市約有12萬人出行，若將A，B，C這三類出行方式均視為“綠色出行”方式，請估計該市“綠色出行”方式的人數(shù)．

【考點】VC：條形統(tǒng)計圖；V5：用樣本估計總體；VA：統(tǒng)計表；VB：扇形統(tǒng)計圖．

【分析】（1）由C類別人數(shù)及其百分比可得總?cè)藬?shù)，總?cè)藬?shù)乘以B類別百分比即可得；

（2）根據(jù)百分比之和為1求得A類別百分比，再乘以360°和總?cè)藬?shù)可分別求得；

（3）總?cè)藬?shù)乘以樣本中A、B、C三類別百分比之和可得答案．

【解答】解：（1）本次調(diào)查的市民有200÷25%=800（人），

∴B類別的人數(shù)為800×30%=240（人），

故答案為：800，240；

（2）∵A類人數(shù)所占百分比為1﹣（30%+25%+14%+6%）=25%，

∴A類對應(yīng)扇形圓心角α的度數(shù)為360°×25%=90°，A類的人數(shù)為800×25%=200（人），

補全條形圖如下：

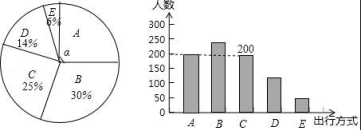
（3）12×（25%+30%+25%）=9.6（萬人），

答：估計該市“綠色出行”方式的人數(shù)約為9.6萬人．

19．如圖，是一種斜挎包，其挎帶由雙層部分、單層部分和調(diào)節(jié)扣構(gòu)成．小敏用后發(fā)現(xiàn)，通過調(diào)節(jié)扣加長或縮短單層部分的長度，可以使挎帶的長度（單層部分與雙層部分長度的和，其中調(diào)節(jié)扣所占的長度忽略不計）加長或縮短．設(shè)單層部分的長度為xcm，雙層部分的長度為ycm，經(jīng)測量，得到如下數(shù)據(jù)：

（1）根據(jù)表中數(shù)據(jù)的規(guī)律，完成以下表格，并直接寫出y關(guān)于x的函數(shù)解析式；

（2）根據(jù)小敏的身高和習(xí)慣，挎帶的長度為120cm時，背起來正合適，請求出此時單層部分的長度；

（3）設(shè)挎帶的長度為lcm，求l的取值范圍．

【考點】FH：一次函數(shù)的應(yīng)用．

【分析】（1）觀察表格可知，y是x使得一次函數(shù)，設(shè)y=kx+b，利用待定系數(shù)法即可解決問題；

（2）列出方程組即可解決問題；

（3）由題意當(dāng)y=0，x=150，當(dāng)x=0時，y=75，可得75≤l≤150．

【解答】解：（1）觀察表格可知，y是x使得一次函數(shù)，設(shè)y=kx+b，

則有，解得，

∴y=﹣x+75．

（2）由題意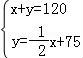，解得，

∴單層部分的長度為90cm．

（3）由題意當(dāng)y=0，x=150，當(dāng)x=0時，y=75，

∴75≤l≤150．

20．如圖，直線y=k1x（x≥0）與雙曲線y=（x＞0）相交于點P（2，4）．已知點A（4，0），B（0，3），連接AB，將Rt△AOB沿OP方向平移，使點O移動到點P，得到△A'PB'．過點A'作A'C∥y軸交雙曲線于點C．

（1）求k1與k2的值；

（2）求直線PC的表達式；

（3）直接寫出線段AB掃過的面積．

【考點】G8：反比例函數(shù)與一次函數(shù)的交點問題；FA：待定系數(shù)法求一次函數(shù)解析式；Q3：坐標(biāo)與圖形變化﹣平移．

【分析】（1）把點P（2，4）代入直線y=k1x，把點P（2，4）代入雙曲線y=，可得k1與k2的值；

（2）根據(jù)平移的性質(zhì)，求得C（6，），再運用待定系數(shù)法，即可得到直線PC的表達式；

（3）延長A'C交x軸于D，過B'作B'E⊥y軸于E，根據(jù)△AOB≌△A'PB'，可得線段AB掃過的面積=平行四邊形POBB'的面積+平行四邊形AOPA'的面積，據(jù)此可得線段AB掃過的面積．

【解答】解：（1）把點P（2，4）代入直線y=k1x，可得4=2k1，

∴k1=2，

把點P（2，4）代入雙曲線y=，可得k2=2×4=8；

（2）∵A（4，0），B（0，3），

∴AO=4，BO=3，

如圖，延長A'C交x軸于D，

由平移可得，A'P=AO=4，

又∵A'C∥y軸，P（2，4），

∴點C的橫坐標(biāo)為2+4=6，

當(dāng)x=6時，y==，即C（6，），

設(shè)直線PC的解析式為y=kx+b，

把P（2，4），C（6，）代入可得

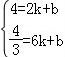，解得，

∴直線PC的表達式為y=﹣x+；

（3）如圖，延長A'C交x軸于D，

由平移可得，A'P∥AO，

又∵A'C∥y軸，P（2，4），

∴點A'的縱坐標(biāo)為4，即A'D=4，

如圖，過B'作B'E⊥y軸于E，

∵PB'∥y軸，P（2，4），

∴點B'的橫坐標(biāo)為2，即B'E=2，

又∵△AOB≌△A'PB'，

∴線段AB掃過的面積=平行四邊形POBB'的面積+平行四邊形AOPA'的面積=BO×B'E+AO×A'D=3×2+4×4=22．

五、（本大題共2小題，每小題9分，共18分）.

21．如圖1，⊙O的直徑AB=12，P是弦BC上一動點（與點B，C不重合），∠ABC=30°，過點P作PD⊥OP交⊙O于點D．

（1）如圖2，當(dāng)PD∥AB時，求PD的長；

（2）如圖3，當(dāng)=時，延長AB至點E，使BE=AB，連接DE．

①求證：DE是⊙O的切線；

②求PC的長．

【考點】MR：圓的綜合題．

【分析】（1）根據(jù)題意首先得出半徑長，再利用銳角三角三角函數(shù)關(guān)系得出OP，PD的長；

（2）①首先得出△OBD是等邊三角形，進而得出∠ODE=∠OFB=90°，求出答案即可；

②首先求出CF的長，進而利用直角三角形的性質(zhì)得出PF的長，進而得出答案．

【解答】解：（1）如圖2，連接OD，

∵OP⊥PD，PD∥AB，

∴∠POB=90°，

∵⊙O的直徑AB=12，

∴OB=OD=6，

在Rt△POB中，∠ABC=30°，

∴OP=OB?tan30°=6×=2，

在Rt△POD中，

PD===2；

（2）①證明：如圖3，連接OD，交CB于點F，連接BD，

∵=，

∴∠DBC=∠ABC=30°，

∴∠ABD=60°，

∵OB=OD，

∴△OBD是等邊三角形，

∴OD⊥FB，

∵BE=AB，

∴OB=BE，

∴BF∥ED，

∴∠ODE=∠OFB=90°，

∴DE是⊙O的切線；

②由①知，OD⊥BC，

∴CF=FB=OB?cos30°=6×=3，

在Rt△POD中，OF=DF，

∴PF=DO=3（直角三角形斜邊上的中線，等于斜邊的一半），

∴CP=CF﹣PF=3﹣3．

22．已知拋物線C1：y=ax2﹣4ax﹣5（a＞0）．

（1）當(dāng)a=1時，求拋物線與x軸的交點坐標(biāo)及對稱軸；

（2）①試說明無論a為何值，拋物線C1一定經(jīng)過兩個定點，并求出這兩個定點的坐標(biāo)；

②將拋物線C1沿這兩個定點所在直線翻折，得到拋物線C2，直接寫出C2的表達式；

（3）若（2）中拋物線C2的頂點到x軸的距離為2，求a的值．

【考點】HA：拋物線與x軸的交點；H6：二次函數(shù)圖象與幾何變換．

【分析】（1）將a=1代入解析式，即可求得拋物線與x軸交點；

（2）①化簡拋物線解析式，即可求得兩個點定點的橫坐標(biāo)，即可解題；

②根據(jù)拋物線翻折理論即可解題；

（3）根據(jù)（2）中拋物線C2解析式，分類討論y=2或﹣2，即可解題；

【解答】解：（1）當(dāng)a=1時，拋物線解析式為y=x2﹣4x﹣5=（x﹣2）2﹣9，

∴對稱軸為y=2；

∴當(dāng)y=0時，x﹣2=3或﹣3，即x=﹣1或5；

∴拋物線與x軸的交點坐標(biāo)為（﹣1，0）或（5，0）；

（2）①拋物線C1解析式為：y=ax2﹣4ax﹣5，

整理得：y=ax（x﹣4）﹣5；

∵當(dāng)ax（x﹣4）=0時，y恒定為﹣5；

∴拋物線C1一定經(jīng)過兩個定點（0，﹣5），（4，﹣5）；

②這兩個點連線為y=﹣5；

將拋物線C1沿y=﹣5翻折，得到拋物線C2，開口方向變了，但是對稱軸沒變；

∴拋物線C2解析式為：y=﹣ax2+4ax﹣5，

（3）拋物線C2的頂點到x軸的距離為2，

則x=2時，y=2或者﹣2；

當(dāng)y=2時，2=﹣4a+8a﹣5，解得，a=；

當(dāng)y=﹣2時，﹣2=﹣4a+8a﹣5，解得，a=；

∴a=或；

六、（本大題共12分）

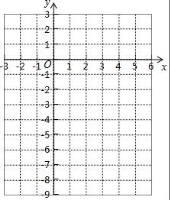
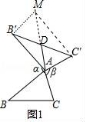
23．我們定義：如圖1，在△ABC看，把AB點繞點A順時針旋轉(zhuǎn)α（0°＜α＜180°）得到AB'，把AC繞點A逆時針旋轉(zhuǎn)β得到AC'，連接B'C'．當(dāng)α+β=180°時，我們稱△A'B'C'是△ABC的“旋補三角形”，△AB'C'邊B'C'上的中線AD叫做△ABC的“旋補中線”，點A叫做“旋補中心”．

特例感知：

（1）在圖2，圖3中，△AB'C'是△ABC的“旋補三角形”，AD是△ABC的“旋補中線”．

①如圖2，當(dāng)△ABC為等邊三角形時，AD與BC的數(shù)量關(guān)系為AD=　　BC；

②如圖3，當(dāng)∠BAC=90°，BC=8時，則AD長為　4　．

猜想論證：

（2）在圖1中，當(dāng)△ABC為任意三角形時，猜想AD與BC的數(shù)量關(guān)系，并給予證明．

拓展應(yīng)用

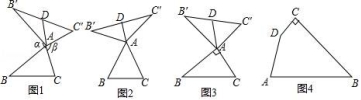
（3）如圖4，在四邊形ABCD，∠C=90°，∠D=150°，BC=12，CD=2，DA=6．在四邊形內(nèi)部是否存在點P，使△PDC是△PAB的“旋補三角形”？若存在，給予證明，并求△PAB的“旋補中線”長；若不存在，說明理由．

【考點】LO：四邊形綜合題．

【分析】（1）①首先證明△ADB′是含有30°是直角三角形，可得AD=AB′即可解決問題；

②首先證明△BAC≌△B′AC′，根據(jù)直角三角形斜邊中線定理即可解決問題；

（2）結(jié)論：AD=BC．如圖1中，延長AD到M，使得AD=DM，連接E′M，C′M，首先證明四邊形AC′MB′是平行四邊形，再證明△BAC≌△AB′M，即可解決問題；

（3）存在．如圖4中，延長AD交BC的延長線于M，作BE⊥AD于E，作線段BC的垂直平分線交BE于P，交BC于F，連接PA、PD、PC，作△PCD的中線PN．連接DF交PC于O．想辦法證明PA=PD，PB=PC，再證明∠APD+∠BPC=180°，即可；

【解答】解：（1）①如圖2中，

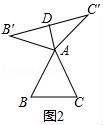
∵△ABC是等邊三角形，

∴AB=BC=AB=AB′=AC′，

∵DB′=DC′，

∴AD⊥B′C′，

∵∠BAC=60°，∠BAC+∠B′AC′=180°，

∴∠B′AC′=120°，

∴∠B′=∠C′=30°，

∴AD=AB′=BC，

故答案為．

②如圖3中，

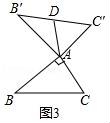
∵∠BAC=90°，∠BAC+∠B′AC′=180°，

∴∠B′AC′=∠BAC=90°，

∵AB=AB′，AC=AC′，

∴△BAC≌△B′AC′，

∴BC=B′C′，

∵B′D=DC′，

∴AD=B′C′=BC=4，

故答案為4．

（2）結(jié)論：AD=BC．

理由：如圖1中，延長AD到M，使得AD=DM，連接E′M，C′M

∵B′D=DC′，AD=DM，

∴四邊形AC′MB′是平行四邊形，

∴AC′=B′M=AC，

∵∠BAC+∠B′AC′=180°，∠B′AC′+∠AB′M=180°，

∴∠BAC=∠MB′A，∵AB=AB′，

∴△BAC≌△AB′M，

∴BC=AM，

∴AD=BC．

（3）存在．

理由：如圖4中，延長AD交BC的延長線于M，作BE⊥AD于E，作線段BC的垂直平分線交BE于P，交BC于F，連接PA、PD、PC，作△PCD的中線PN．

連接DF交PC于O．

∵∠ADC=150°，

∴∠MDC=30°，

在Rt△DCM中，∵CD=2，∠DCM=90°，∠MDC=30°，

∴CM=2，DM=4，∠M=60°，

在Rt△BEM中，∵∠BEM=90°，BM=14，∠MBE=30°，

∴EM=BM=7，

∴DE=EM﹣DM=3，

∵AD=6，

∴AE=DE，∵BE⊥AD，

∴PA=PD，PB=PC，

在Rt△CDF中，∵CD=2，CF=6，

∴tan∠CDF=，

∴∠CDF=60°=∠CPF，

易證△FCP≌△CFD，

∴CD=PF，∵CD∥PF，

∴四邊形CDPF是矩形，

∴∠CDP=90°，

∴∠ADP=∠ADC﹣∠CDP=60°，

∴△ADP是等邊三角形，

∴∠ADP=60°，∵∠BPF=∠CPF=60°，

∴∠BPC=120°，

∴∠APD+∠BPC=180°，

∴△PDC是△PAB的“旋補三角形”，

在Rt△PDN中，∵∠PDN=90°，PD=AD=6，DN=，

∴PN===．

2017年7月4日