2017年廣東省惠州市惠陽(yáng)區(qū)中考數(shù)學(xué)模擬試卷題【精編解析版】

由于版式的問(wèn)題，試題可能會(huì)出現(xiàn)亂碼的現(xiàn)象，為了方便您的閱讀請(qǐng)點(diǎn)擊全屏查看

一．選擇題（共10小題，每小題3分，共30分．）

1．的倒數(shù)是（）

A．﹣2????????????? B．2????????????? C．????????????? D．

2．下列圖案中既是中心對(duì)稱(chēng)圖形，又是軸對(duì)稱(chēng)圖形的是（）

A．????????????? B．????????????? C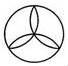．????????????? D．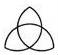

3．中國(guó)倡導(dǎo)的“一帶一路”建設(shè)將促進(jìn)我國(guó)與世界各國(guó)的互利合作，根據(jù)規(guī)劃，“一帶一路”地區(qū)覆蓋總?cè)丝诩s為4400000000人，這個(gè)數(shù)用科學(xué)記數(shù)法表示為（）

A．44×108????????????? B．4.4×109????????????? C．4.4×108????????????? D．4.4×1010

4．2010年3月份，某市市區(qū)一周空氣質(zhì)量報(bào)告中某項(xiàng)污染指數(shù)的數(shù)據(jù)是：31，35，31，34，30，32，31，這組數(shù)據(jù)的中位數(shù)、眾數(shù)分別是（）

A．32，31????????????? B．31，32????????????? C．31，31????????????? D．32，35

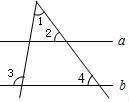
5．如圖，直線(xiàn)a∥b，若∠2=55°，∠3=100°，則∠1的度數(shù)為（）

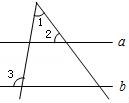
A．35°????????????? B．45°????????????? C．50°????????????? D．55°

6．下列運(yùn)算正確的是（）

A．2a+3b=5ab????????????? B．a(chǎn)2?a3=a5????????????? C．（2a）3=6a 3????????????? D．a(chǎn)6+a3=a9

7．一元二次方程x2﹣4x+2=0的根的情況是（）

A．有兩個(gè)不相等的實(shí)數(shù)根????????????? B．有兩個(gè)相等的實(shí)數(shù)根

C．只有一個(gè)實(shí)數(shù)根????????????? D．沒(méi)有實(shí)數(shù)根

8．若等腰三角形的兩邊長(zhǎng)為3和7，則該等腰三角形的周長(zhǎng)為（）

A．10????????????? B．13????????????? C．17????????????? D．13或17

9．不等式組的解集在數(shù)軸上表示正確的是（）

A．????????????? B．????????????? C．????????????? D．

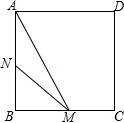
10．如圖，正方形ABCD的邊長(zhǎng)為3cm，動(dòng)點(diǎn)M從點(diǎn)B出發(fā)以3cm/s的速度沿著邊BC﹣CD﹣DA運(yùn)動(dòng)，到達(dá)點(diǎn)A停止運(yùn)動(dòng)，另一動(dòng)點(diǎn)N同時(shí)從點(diǎn)B出發(fā)，以1cm/s的速度沿著邊BA向點(diǎn)A運(yùn)動(dòng)，到達(dá)點(diǎn)A停止運(yùn)動(dòng)，設(shè)點(diǎn)M運(yùn)動(dòng)時(shí)間為x（s），△AMN的面積為y（cm2），則y關(guān)于x的函數(shù)圖象是（）

A．????????????? B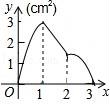．????????????? C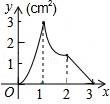．????????????? D．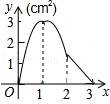

二、填空題（本題共6小題，每小題4分，共24分）

11．因式分解：x2﹣36=　?? 　．

12．一個(gè)多邊形的內(nèi)角和為1080°，則這個(gè)多邊形的邊數(shù)是　?? 　．

13．若△ABC∽△A′B′C′，相似比為1：3，則△ABC與△A′B′C′的面積之比為　?? 　．

14．分式方程的解是　?? 　．

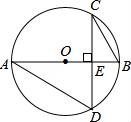
15．如圖，在⊙O中，CD⊥AB于E，若∠BAD=30°，且BE=2，則CD=　?? 　．

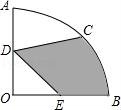
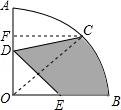
16．如圖，在圓心角為90°的扇形OAB中，半徑OA=4，C為的中點(diǎn)，D、E分別為OA，OB的中點(diǎn)，則圖中陰影部分的面積為　?? 　．

三、解答題（本題共3小題，每小題6分，共18分）

17．計(jì)算：（﹣）﹣1﹣|﹣1|+3tan30°+0．

18．先化簡(jiǎn)，再求值：

（），請(qǐng)?jiān)讴?，0，1，3中選擇一個(gè)適當(dāng)?shù)臄?shù)作為x值．

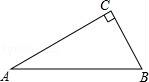
19．如圖，△ABC中，∠C=90°，∠A=30°．

（1）用尺規(guī)作圖作AB邊上的垂直平分線(xiàn)DE，交AC于點(diǎn)D，交AB于點(diǎn)E．（保留作圖痕跡，不要求寫(xiě)作法和證明）

（2）連接BD，求證：DE=CD．

四、解答題（本題共3小題，每小題7分，共21分）

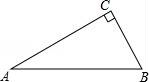
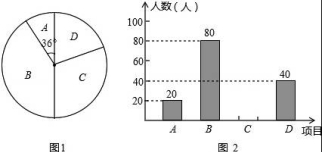
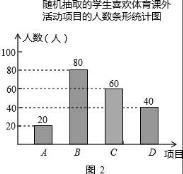
20．某學(xué)校為了增強(qiáng)學(xué)生體質(zhì)，決定開(kāi)設(shè)以下體育課外活動(dòng)項(xiàng)目：A籃球、B乒乓球、C跳繩、D踢毽子，為了解學(xué)生最喜歡哪一種活動(dòng)項(xiàng)目，隨機(jī)抽取了部分學(xué)生進(jìn)行調(diào)查，并將調(diào)查結(jié)果繪制成了兩幅不完整的統(tǒng)計(jì)圖，請(qǐng)回答下列問(wèn)題：

（1）這次被調(diào)查的學(xué)生共有　?? 　人；

（2）請(qǐng)你將條形統(tǒng)計(jì)圖補(bǔ)充完成；

（3）在平時(shí)的乒乓球項(xiàng)目訓(xùn)練中，甲、乙、丙、丁四人表現(xiàn)優(yōu)秀，現(xiàn)決定從這四名同學(xué)中任選兩名參加乒乓球比賽，求恰好選中甲、乙兩位同學(xué)的概率（用樹(shù)狀圖或列表法解答）．

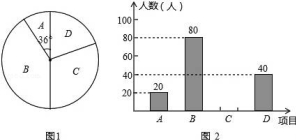
21．為促進(jìn)我市經(jīng)濟(jì)的快速發(fā)展，加快道路建設(shè)，某高速公路建設(shè)工程中需修隧道AB，如圖，在山外一點(diǎn)C測(cè)得BC距離為200m，∠CAB=54°，∠CBA=30°，求隧道AB的長(zhǎng)．（參考數(shù)據(jù)：sin54°≈0.81，cos54°≈0.59，tan54°≈1.38，≈1.73，精確到個(gè)位）

22．某種商品的標(biāo)價(jià)為400元/件，經(jīng)過(guò)兩次降價(jià)后的價(jià)格為324元/件，并且兩次降價(jià)的百分率相同．

（1）求該種商品每次降價(jià)的百分率；

（2）若該種商品進(jìn)價(jià)為300元/件，兩次降價(jià)共售出此種商品100件，為使兩次降價(jià)銷(xiāo)售的總利潤(rùn)不少于3210元．問(wèn)第一次降價(jià)后至少要售出該種商品多少件？

五、解答題（本題共3小題，每小題9分，共27分）

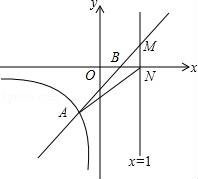
23．直線(xiàn)y=kx+b與反比例函數(shù)y=（x＜0）的圖象交于點(diǎn)A（﹣1，m），與x軸交于點(diǎn)B（1，0）

（1）求m的值；

（2）求直線(xiàn)AB的解析式；

（3）若直線(xiàn)x=t（t＞1）與直線(xiàn)y=kx+b交于點(diǎn)M，與x軸交于點(diǎn)N，連接AN，S△AMN=，求t的值．

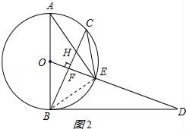
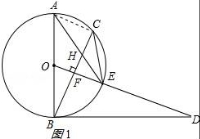
24．已知，如圖，AB是⊙O的直徑，點(diǎn)C為⊙O上一點(diǎn)，OF⊥BC于點(diǎn)F，交⊙O于點(diǎn)E，AE與BC交于點(diǎn)H，點(diǎn)D為OE的延長(zhǎng)線(xiàn)上一點(diǎn)，且∠ODB=∠AEC．

（1）求證：BD是⊙O的切線(xiàn)；

（2）求證：CE2=EH?EA；

（3）若⊙O的半徑為5，sinA=，求BH的長(zhǎng)．

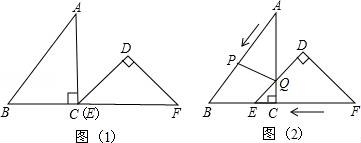
25．把Rt△ABC和Rt△DEF按如圖（1）擺放（點(diǎn)C與E重合），點(diǎn)B、C（E）、F在同一條直線(xiàn)上．已知：∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=10cm．如圖（2），△DEF從圖（1）的位置出發(fā)，以1cm/s的速度沿CB向△ABC勻速移動(dòng)，在△DEF移動(dòng)的同時(shí)，點(diǎn)P從△ABC的頂點(diǎn)A出發(fā)，以2cm/s的速度沿AB向點(diǎn)B勻速移動(dòng)；當(dāng)點(diǎn)P移動(dòng)到點(diǎn)B時(shí)，點(diǎn)P停止移動(dòng)，△DEF也隨之停止移動(dòng)．DE與AC交于點(diǎn)Q，連接PQ，設(shè)移動(dòng)時(shí)間為t（s）．

（1）用含t的代數(shù)式表示線(xiàn)段AP和AQ的長(zhǎng)，并寫(xiě)出t的取值范圍；

（2）連接PE，設(shè)四邊形APEQ的面積為y（cm2），試探究y的最大值；

（3）當(dāng)t為何值時(shí)，△APQ是等腰三角形．

2017年廣東省惠州市惠陽(yáng)區(qū)中考數(shù)學(xué)模擬試卷題參考答案與試題解析

一．選擇題（共10小題，每小題3分，共30分．）

1．的倒數(shù)是（）

A．﹣2????????????? B．2????????????? C．????????????? D．

【考點(diǎn)】17：倒數(shù)．

【分析】根據(jù)倒數(shù)的定義求解．

【解答】解：﹣的倒數(shù)是﹣2．

故選：A．

2．下列圖案中既是中心對(duì)稱(chēng)圖形，又是軸對(duì)稱(chēng)圖形的是（）

A．????????????? B．????????????? C．????????????? D．

【考點(diǎn)】R5：中心對(duì)稱(chēng)圖形；P3：軸對(duì)稱(chēng)圖形．

【分析】根據(jù)中心對(duì)稱(chēng)圖形的定義旋轉(zhuǎn)180°后能夠與原圖形完全重合即是中心對(duì)稱(chēng)圖形，以及軸對(duì)稱(chēng)圖形的定義即可判斷出．

【解答】解：A、∵此圖形旋轉(zhuǎn)180°后不能與原圖形重合，∴此圖形不是中心對(duì)稱(chēng)圖形，是軸對(duì)稱(chēng)圖形，故此選項(xiàng)錯(cuò)誤；

B、∵此圖形旋轉(zhuǎn)180°后能與原圖形重合，∴此圖形是中心對(duì)稱(chēng)圖形，也是軸對(duì)稱(chēng)圖形，故此選項(xiàng)正確；

C、∵此圖形旋轉(zhuǎn)180°后不能與原圖形重合，∴此圖形不是中心對(duì)稱(chēng)圖形，是軸對(duì)稱(chēng)圖形，故此選項(xiàng)錯(cuò)誤；

D、∵此圖形旋轉(zhuǎn)180°后不能與原圖形重合，∴此圖形不是中心對(duì)稱(chēng)圖形，是軸對(duì)稱(chēng)圖形，故此選項(xiàng)錯(cuò)誤．

故選：B．

3．中國(guó)倡導(dǎo)的“一帶一路”建設(shè)將促進(jìn)我國(guó)與世界各國(guó)的互利合作，根據(jù)規(guī)劃，“一帶一路”地區(qū)覆蓋總?cè)丝诩s為4400000000人，這個(gè)數(shù)用科學(xué)記數(shù)法表示為（）

A．44×108????????????? B．4.4×109????????????? C．4.4×108????????????? D．4.4×1010

【考點(diǎn)】1I：科學(xué)記數(shù)法—表示較大的數(shù)．

【分析】科學(xué)記數(shù)法的表示形式為a×10n的形式，其中1≤|a|＜10，n為整數(shù)．確定n的值時(shí)，要看把原數(shù)變成a時(shí)，小數(shù)點(diǎn)移動(dòng)了多少位，n的絕對(duì)值與小數(shù)點(diǎn)移動(dòng)的位數(shù)相同．當(dāng)原數(shù)絕對(duì)值＞1時(shí)，n是正數(shù)；當(dāng)原數(shù)的絕對(duì)值＜1時(shí)，n是負(fù)數(shù)．

【解答】解：4 400 000 000=4.4×109，

故選：B．

4．2010年3月份，某市市區(qū)一周空氣質(zhì)量報(bào)告中某項(xiàng)污染指數(shù)的數(shù)據(jù)是：31，35，31，34，30，32，31，這組數(shù)據(jù)的中位數(shù)、眾數(shù)分別是（）

A．32，31????????????? B．31，32????????????? C．31，31????????????? D．32，35

【考點(diǎn)】W5：眾數(shù)；W4：中位數(shù)．

【分析】利用中位數(shù)及眾數(shù)的定義確定答案即可．

【解答】解：∵數(shù)據(jù)31出現(xiàn)了3次，最多，

∴眾數(shù)為31，

∵排序后位于中間位置的數(shù)是31，

∴中位數(shù)是31，

故選C．

5．如圖，直線(xiàn)a∥b，若∠2=55°，∠3=100°，則∠1的度數(shù)為（）

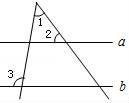
A．35°????????????? B．45°????????????? C．50°????????????? D．55°

【考點(diǎn)】JA：平行線(xiàn)的性質(zhì)．

【分析】根據(jù)兩直線(xiàn)平行，同位角相等可得∠4=∠2，再根據(jù)三角形的一個(gè)外角等于與它不相鄰的兩個(gè)內(nèi)角的和列式計(jì)算即可得解．

【解答】解：如圖，∵直線(xiàn)a∥b，

∴∠4=∠2=55°，

∴∠1=∠3﹣∠4=100°﹣55°=45°．

故選B．

6．下列運(yùn)算正確的是（）

A．2a+3b=5ab????????????? B．a(chǎn)2?a3=a5????????????? C．（2a）3=6a 3????????????? D．a(chǎn)6+a3=a9

【考點(diǎn)】47：冪的乘方與積的乘方；35：合并同類(lèi)項(xiàng)；46：同底數(shù)冪的乘法．

【分析】直接利用合并同類(lèi)項(xiàng)法則以及結(jié)合冪的乘方與積的乘方法則，分別化簡(jiǎn)求出答案．

【解答】解：A、2a+3b無(wú)法計(jì)算，故此選項(xiàng)不合題意；

B、a2?a3=a5，正確，符合題意；

C、（2a）3=8a 3，故此選項(xiàng)不合題意；

D、a6+a3，無(wú)法計(jì)算，故此選項(xiàng)不合題意；

故選：B．

7．一元二次方程x2﹣4x+2=0的根的情況是（）

A．有兩個(gè)不相等的實(shí)數(shù)根????????????? B．有兩個(gè)相等的實(shí)數(shù)根

C．只有一個(gè)實(shí)數(shù)根????????????? D．沒(méi)有實(shí)數(shù)根

【考點(diǎn)】AA：根的判別式．

【分析】先計(jì)算出判別式的值，然后根據(jù)判別式的意義判定方程解的情況．

【解答】解：∵△=（﹣4）2﹣4×2=8＞0，

∴方程有兩個(gè)不相等的實(shí)數(shù)根．

故選A．

8．若等腰三角形的兩邊長(zhǎng)為3和7，則該等腰三角形的周長(zhǎng)為（）

A．10????????????? B．13????????????? C．17????????????? D．13或17

【考點(diǎn)】KH：等腰三角形的性質(zhì)；K6：三角形三邊關(guān)系．

【分析】因?yàn)榈妊切蔚膬蛇厼?和7，但已知中沒(méi)有點(diǎn)明底邊和腰，所以有兩種情況，需要分類(lèi)討論，還要注意利用三角形三邊關(guān)系考查各情況能否構(gòu)成三角形．

【解答】解：當(dāng)3為底時(shí)，其它兩邊都為7，3、7、7可以構(gòu)成三角形，周長(zhǎng)為17；

當(dāng)3為腰時(shí)，其它兩邊為3和7，

∵3+3=6＜7，

所以不能構(gòu)成三角形，故舍去，

∴答案只有17．

故選C．

9．不等式組的解集在數(shù)軸上表示正確的是（）

A．????????????? B．????????????? C．????????????? D．

【考點(diǎn)】C4：在數(shù)軸上表示不等式的解集；CB：解一元一次不等式組．

【分析】先求出不等式組中每一個(gè)不等式的解集，再求出它們的公共部分，然后把不等式的解集表示在數(shù)軸上即可．

【解答】解：由x＞﹣1，得x＞﹣1，

由2x≤4，得x≤2，

∴不等式組的解集是﹣1＜x≤2，

故選：B．

10．如圖，正方形ABCD的邊長(zhǎng)為3cm，動(dòng)點(diǎn)M從點(diǎn)B出發(fā)以3cm/s的速度沿著邊BC﹣CD﹣DA運(yùn)動(dòng)，到達(dá)點(diǎn)A停止運(yùn)動(dòng)，另一動(dòng)點(diǎn)N同時(shí)從點(diǎn)B出發(fā)，以1cm/s的速度沿著邊BA向點(diǎn)A運(yùn)動(dòng)，到達(dá)點(diǎn)A停止運(yùn)動(dòng)，設(shè)點(diǎn)M運(yùn)動(dòng)時(shí)間為x（s），△AMN的面積為y（cm2），則y關(guān)于x的函數(shù)圖象是（）

A．????????????? B．????????????? C．????????????? D．

【考點(diǎn)】E7：動(dòng)點(diǎn)問(wèn)題的函數(shù)圖象．

【分析】分三種情況進(jìn)行討論，當(dāng)0≤x≤1時(shí)，當(dāng)1≤x≤2時(shí)，當(dāng)2≤x≤3時(shí)，分別求得△ANM的面積，列出函數(shù)解析式，根據(jù)函數(shù)圖象進(jìn)行判斷即可．

【解答】解：由題可得，BN=x，

當(dāng)0≤x≤1時(shí)，M在BC邊上，BM=3x，AN=3﹣x，則

S△ANM=AN?BM，

∴y=?（3﹣x）?3x=﹣x2+x，故C選項(xiàng)錯(cuò)誤；

當(dāng)1≤x≤2時(shí)，M點(diǎn)在CD邊上，則

S△ANM=AN?BC，

∴y=（3﹣x）?3=﹣x+，故D選項(xiàng)錯(cuò)誤；

當(dāng)2≤x≤3時(shí)，M在AD邊上，AM=9﹣3x，

∴S△ANM=AM?AN，

∴y=?（9﹣3x）?（3﹣x）=（x﹣3）2，故B選項(xiàng)錯(cuò)誤；

故選（A）．

二、填空題（本題共6小題，每小題4分，共24分）

11．因式分解：x2﹣36=　（x+6）（x﹣6）　．

【考點(diǎn)】54：因式分解﹣運(yùn)用公式法．

【分析】直接用平方差公式分解．平方差公式：a2﹣b2=（a+b）（a﹣b）．

【解答】解：x2﹣36=（x+6）（x﹣6）．

12．一個(gè)多邊形的內(nèi)角和為1080°，則這個(gè)多邊形的邊數(shù)是　8　．

【考點(diǎn)】L3：多邊形內(nèi)角與外角．

【分析】n邊形的內(nèi)角和是（n﹣2）?180°，如果已知多邊形的邊數(shù)，就可以得到一個(gè)關(guān)于邊數(shù)的方程，解方程就可以求出多邊形的邊數(shù)．

【解答】解：根據(jù)n邊形的內(nèi)角和公式，得

（n﹣2）?180=1080，

解得n=8．

∴這個(gè)多邊形的邊數(shù)是8．

故答案為：8．

13．若△ABC∽△A′B′C′，相似比為1：3，則△ABC與△A′B′C′的面積之比為　1：9　．

【考點(diǎn)】S7：相似三角形的性質(zhì)．

【分析】根據(jù)相似三角形面積的比等于相似比的平方解答．

【解答】解：∵△ABC∽△A′B′C′，相似比為1：3，

∴△ABC與△A′B′C′的面積之比為1：9．

故答案為：1：9．

14．分式方程的解是　x=﹣1　．

【考點(diǎn)】B2：分式方程的解．

【分析】根據(jù)解分式方程的方法可以求得分式方程的解，記住最后要進(jìn)行檢驗(yàn)，本題得以解決．

【解答】解：

方程兩邊同乘以2x（x﹣3），得

x﹣3=4x

解得，x=﹣1，

檢驗(yàn)：當(dāng)x=﹣1時(shí)，2x（x﹣3）≠0，

故原分式方程的解是x=﹣1，

故答案為：x=﹣1．

15．如圖，在⊙O中，CD⊥AB于E，若∠BAD=30°，且BE=2，則CD=　4　．

【考點(diǎn)】M2：垂徑定理；M5：圓周角定理．

【分析】先根據(jù)圓周角定理求出∠C的度數(shù)，再由CD⊥AB可知∠CEB=90°，CD=2CE，由直角三角形的性質(zhì)求出BC的長(zhǎng)，根據(jù)勾股定理求出CE的長(zhǎng)，進(jìn)而可得出結(jié)論．

【解答】解：∵∠BAD=30°，BE=2，

∴∠C=∠BAD=30°．

∵CD⊥AB，

∴∠CEB=90°，CD=2CE，

∴BC=2BE=4，

∴CE===2，

∴CD=2CE=4．

故答案為：4．

16．如圖，在圓心角為90°的扇形OAB中，半徑OA=4，C為的中點(diǎn)，D、E分別為OA，OB的中點(diǎn)，則圖中陰影部分的面積為　2π+2﹣2　．

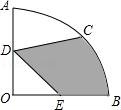
【考點(diǎn)】MO：扇形面積的計(jì)算．

【分析】連接OC、EC，由△OCD≌△OCE、OC⊥DE可得DE==2，分別求出S扇形OBC、S△OCD、S△ODE面積，根據(jù)S扇形OBC+S△OCD﹣S△ODE=S陰影部分可得．

【解答】解：連結(jié)OC，過(guò)C點(diǎn)作CF⊥OA于F，

∵半徑OA=4，C為的中點(diǎn)，D、E分別是OA、OB的中點(diǎn)，

∴OD=OE=2，OC=4，∠AOC=45°，

∴CF=2，

∴空白圖形ACD的面積=扇形OAC的面積﹣三角形OCD的面積

=﹣×2×2

=2π﹣2，

三角形ODE的面積=OD×OE=2，

∴圖中陰影部分的面積=扇形OAB的面積﹣空白圖形ACD的面積﹣三角形ODE的面積

=﹣（2π﹣2）﹣2

=2π+2﹣2．

故答案為：2π+2﹣2．

三、解答題（本題共3小題，每小題6分，共18分）

17．計(jì)算：（﹣）﹣1﹣|﹣1|+3tan30°+0．

【考點(diǎn)】2C：實(shí)數(shù)的運(yùn)算；6E：零指數(shù)冪；6F：負(fù)整數(shù)指數(shù)冪；T5：特殊角的三角函數(shù)值．

【分析】原式利用零指數(shù)冪、負(fù)整數(shù)指數(shù)冪法則，絕對(duì)值的代數(shù)意義，以及特殊角的三角函數(shù)值計(jì)算即可得到結(jié)果．

【解答】解：原式=﹣4﹣+1+3×+1=﹣2．

18．先化簡(jiǎn)，再求值：

（），請(qǐng)?jiān)讴?，0，1，3中選擇一個(gè)適當(dāng)?shù)臄?shù)作為x值．

【考點(diǎn)】6D：分式的化簡(jiǎn)求值．

【分析】先把括號(hào)內(nèi)通分，再把分子分母因式分解和除法運(yùn)算化為乘法運(yùn)算，然后約分得到原式=3x+15，再根據(jù)分式有意義的條件把x=1代入計(jì)算即可．

【解答】解：原式=?

=?

=3x+15，

當(dāng)x=1時(shí)，原式=3+15=18．

19．如圖，△ABC中，∠C=90°，∠A=30°．

（1）用尺規(guī)作圖作AB邊上的垂直平分線(xiàn)DE，交AC于點(diǎn)D，交AB于點(diǎn)E．（保留作圖痕跡，不要求寫(xiě)作法和證明）

（2）連接BD，求證：DE=CD．

【考點(diǎn)】N2：作圖—基本作圖；KG：線(xiàn)段垂直平分線(xiàn)的性質(zhì)；KO：含30度角的直角三角形．

【分析】（1）利用基本作圖（作已知線(xiàn)段的垂直平分線(xiàn)）作DE垂直平分AB；

（2）先利用線(xiàn)段垂直平分線(xiàn)的性質(zhì)得到DA=DB，則∠DBA=∠A=30°，再證明BD平分∠ABC，然后根據(jù)角平分線(xiàn)的性質(zhì)定理可得到結(jié)論．

【解答】（1）解：如圖，DE為所作；

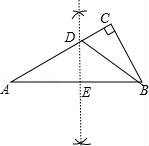
（2）證明：如圖，

∵DE垂直平分AB，

∴DA=DB，

∴∠DBA=∠A=30°，

∵∠ABC=90°﹣∠A=60°，

∴∠CBD=30°，

即BD平分∠ABC，

而DE⊥AB，DC⊥BC，

∴DE=DC．

四、解答題（本題共3小題，每小題7分，共21分）

20．某學(xué)校為了增強(qiáng)學(xué)生體質(zhì)，決定開(kāi)設(shè)以下體育課外活動(dòng)項(xiàng)目：A籃球、B乒乓球、C跳繩、D踢毽子，為了解學(xué)生最喜歡哪一種活動(dòng)項(xiàng)目，隨機(jī)抽取了部分學(xué)生進(jìn)行調(diào)查，并將調(diào)查結(jié)果繪制成了兩幅不完整的統(tǒng)計(jì)圖，請(qǐng)回答下列問(wèn)題：

（1）這次被調(diào)查的學(xué)生共有　200　人；

（2）請(qǐng)你將條形統(tǒng)計(jì)圖補(bǔ)充完成；

（3）在平時(shí)的乒乓球項(xiàng)目訓(xùn)練中，甲、乙、丙、丁四人表現(xiàn)優(yōu)秀，現(xiàn)決定從這四名同學(xué)中任選兩名參加乒乓球比賽，求恰好選中甲、乙兩位同學(xué)的概率（用樹(shù)狀圖或列表法解答）．

【考點(diǎn)】X6：列表法與樹(shù)狀圖法；VB：扇形統(tǒng)計(jì)圖；VC：條形統(tǒng)計(jì)圖．

【分析】（1）由題意可知這次被調(diào)查的學(xué)生共有20÷=200（人）；

（2）首先求得C項(xiàng)目對(duì)應(yīng)人數(shù)為：200﹣20﹣80﹣40=60（人），繼而可補(bǔ)全條形統(tǒng)計(jì)圖；

（3）首先根據(jù)題意畫(huà)出樹(shù)狀圖，然后由樹(shù)狀圖求得所有等可能的結(jié)果與恰好選中甲、乙兩位同學(xué)的情況，再利用概率公式即可求得答案．

【解答】解：（1）根據(jù)題意得：這次被調(diào)查的學(xué)生共有20÷=200（人）．

故答案為：200；

（2）C項(xiàng)目對(duì)應(yīng)人數(shù)為：200﹣20﹣80﹣40=60（人）；

補(bǔ)充如圖．

（3）列表如下：

∵共有12種等可能的情況，恰好選中甲、乙兩位同學(xué)的有2種，

∴P（選中甲、乙）==．

21．為促進(jìn)我市經(jīng)濟(jì)的快速發(fā)展，加快道路建設(shè)，某高速公路建設(shè)工程中需修隧道AB，如圖，在山外一點(diǎn)C測(cè)得BC距離為200m，∠CAB=54°，∠CBA=30°，求隧道AB的長(zhǎng)．（參考數(shù)據(jù)：sin54°≈0.81，cos54°≈0.59，tan54°≈1.38，≈1.73，精確到個(gè)位）

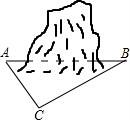
【考點(diǎn)】T8：解直角三角形的應(yīng)用．

【分析】首先過(guò)點(diǎn)C作CD⊥AB于D，然后在Rt△BCD中，利用三角函數(shù)的知識(shí)，求得BD，CD的長(zhǎng)，繼而在Rt△ACD中，利用∠CAB的正切求得AD的長(zhǎng)，繼而求得答案．

【解答】解：過(guò)點(diǎn)C作CD⊥AB于D，

∵BC=200m，∠CBA=30°，

∴在Rt△BCD中，CD=BC=100m，BD=BC?cos30°=200×=100≈173（m），

∵∠CAB=54°，

在Rt△ACD中，AD=≈≈72（m），

∴AB=AD+BD=173+72≈245（m）．

答：隧道AB的長(zhǎng)為245m．

22．某種商品的標(biāo)價(jià)為400元/件，經(jīng)過(guò)兩次降價(jià)后的價(jià)格為324元/件，并且兩次降價(jià)的百分率相同．

（1）求該種商品每次降價(jià)的百分率；

（2）若該種商品進(jìn)價(jià)為300元/件，兩次降價(jià)共售出此種商品100件，為使兩次降價(jià)銷(xiāo)售的總利潤(rùn)不少于3210元．問(wèn)第一次降價(jià)后至少要售出該種商品多少件？

【考點(diǎn)】AD：一元二次方程的應(yīng)用；C9：一元一次不等式的應(yīng)用．

【分析】（1）設(shè)該種商品每次降價(jià)的百分率為x%，根據(jù)“兩次降價(jià)后的售價(jià)=原價(jià)×（1﹣降價(jià)百分比）的平方”，即可得出關(guān)于x的一元二次方程，解方程即可得出結(jié)論；

（2）設(shè)第一次降價(jià)后售出該種商品m件，則第二次降價(jià)后售出該種商品件，根據(jù)“總利潤(rùn)=第一次降價(jià)后的單件利潤(rùn)×銷(xiāo)售數(shù)量+第二次降價(jià)后的單件利潤(rùn)×銷(xiāo)售數(shù)量”，即可得出關(guān)于m的一元一次不等式，解不等式即可得出結(jié)論．

【解答】解：（1）設(shè)該種商品每次降價(jià)的百分率為x%，

依題意得：400×（1﹣x%）2=324，

解得：x=10，或x=190（舍去）．

答：該種商品每次降價(jià)的百分率為10%．

（2）設(shè)第一次降價(jià)后售出該種商品m件，則第二次降價(jià)后售出該種商品件，

第一次降價(jià)后的單件利潤(rùn)為：400×（1﹣10%）﹣300=60（元/件）；

第二次降價(jià)后的單件利潤(rùn)為：324﹣300=24（元/件）．

依題意得：60m+24×=36m+2400≥3210，

解得：m≥22.5．

∴m≥23．

答：為使兩次降價(jià)銷(xiāo)售的總利潤(rùn)不少于3210元．第一次降價(jià)后至少要售出該種商品23件．

五、解答題（本題共3小題，每小題9分，共27分）

23．直線(xiàn)y=kx+b與反比例函數(shù)y=（x＜0）的圖象交于點(diǎn)A（﹣1，m），與x軸交于點(diǎn)B（1，0）

（1）求m的值；

（2）求直線(xiàn)AB的解析式；

（3）若直線(xiàn)x=t（t＞1）與直線(xiàn)y=kx+b交于點(diǎn)M，與x軸交于點(diǎn)N，連接AN，S△AMN=，求t的值．

【考點(diǎn)】G8：反比例函數(shù)與一次函數(shù)的交點(diǎn)問(wèn)題．

【分析】（1）將點(diǎn)A坐標(biāo)代入y=可得m的值；

（2）將點(diǎn)A、B坐標(biāo)代入y=kx+b可得關(guān)于k、b的方程，解方程求出k、b的值，可得直線(xiàn)解析式；

（3）根據(jù)直線(xiàn)直線(xiàn)x=t與直線(xiàn)y=kx+b交于點(diǎn)M、與x軸交于點(diǎn)N表示出M、N的坐標(biāo)，由S△AMN=可得關(guān)于t的方程，解方程可得t的值．

【解答】解：（1）將點(diǎn)A（﹣1，m）代入y=，得：m=﹣2；

（2）由（1）知點(diǎn)A坐標(biāo)為（﹣1，﹣2），

將點(diǎn)A（﹣1，﹣2）、B（1，0）代入y=kx+b，

得：，

解得：，

∴直線(xiàn)AB的解析式為：y=x﹣1；

（3）當(dāng)x=t時(shí)，y=t﹣1，

∴點(diǎn)M坐標(biāo)為（t，t﹣1），點(diǎn)N坐標(biāo)為（t，0），

∵S△AMN=，

∴×（t﹣1）（t+1）=，

解得：t=2或t=﹣2（舍），

∴t=2．

24．已知，如圖，AB是⊙O的直徑，點(diǎn)C為⊙O上一點(diǎn)，OF⊥BC于點(diǎn)F，交⊙O于點(diǎn)E，AE與BC交于點(diǎn)H，點(diǎn)D為OE的延長(zhǎng)線(xiàn)上一點(diǎn)，且∠ODB=∠AEC．

（1）求證：BD是⊙O的切線(xiàn)；

（2）求證：CE2=EH?EA；

（3）若⊙O的半徑為5，sinA=，求BH的長(zhǎng)．

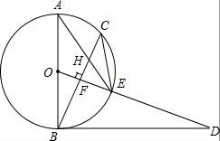
【考點(diǎn)】MR：圓的綜合題．

【分析】（1）由圓周角定理和已知條件證出∠ODB=∠ABC，再證出∠ABC+∠DBF=90°，即∠OBD=90°，即可得出BD是⊙O的切線(xiàn)；

（2）連接AC，由垂徑定理得出，得出∠CAE=∠ECB，再由公共角∠CEA=∠HEC，證明△CEH∽△AEC，得出對(duì)應(yīng)邊成比例，即可得出結(jié)論；

（3）連接BE，由圓周角定理得出∠AEB=90°，由三角函數(shù)求出BE，再根據(jù)勾股定理求出EA，得出BE=CE=6，由（2）的結(jié)論求出EH，然后根據(jù)勾股定理求出BH即可．

【解答】（1）證明：∵∠ODB=∠AEC，∠AEC=∠ABC，

∴∠ODB=∠ABC，

∵OF⊥BC，

∴∠BFD=90°，

∴∠ODB+∠DBF=90°，

∴∠ABC+∠DBF=90°，

即∠OBD=90°，

∴BD⊥OB，

∴BD是⊙O的切線(xiàn)；

（2）證明：連接AC，如圖1所示：

∵OF⊥BC，

∴，

∴∠CAE=∠ECB，

∵∠CEA=∠HEC，

∴△CEH∽△AEC，

∴，

∴CE2=EH?EA；

（3）解：連接BE，如圖2所示：

∵AB是⊙O的直徑，

∴∠AEB=90°，

∵⊙O的半徑為5，sin∠BAE=，

∴AB=10，BE=AB?sin∠BAE=10×=6，

∴EA===8，

∵，

∴BE=CE=6，

∵CE2=EH?EA，

∴EH==，

在Rt△BEH中，BH===．

25．把Rt△ABC和Rt△DEF按如圖（1）擺放（點(diǎn)C與E重合），點(diǎn)B、C（E）、F在同一條直線(xiàn)上．已知：∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=10cm．如圖（2），△DEF從圖（1）的位置出發(fā)，以1cm/s的速度沿CB向△ABC勻速移動(dòng)，在△DEF移動(dòng)的同時(shí)，點(diǎn)P從△ABC的頂點(diǎn)A出發(fā)，以2cm/s的速度沿AB向點(diǎn)B勻速移動(dòng)；當(dāng)點(diǎn)P移動(dòng)到點(diǎn)B時(shí)，點(diǎn)P停止移動(dòng)，△DEF也隨之停止移動(dòng)．DE與AC交于點(diǎn)Q，連接PQ，設(shè)移動(dòng)時(shí)間為t（s）．

（1）用含t的代數(shù)式表示線(xiàn)段AP和AQ的長(zhǎng)，并寫(xiě)出t的取值范圍；

（2）連接PE，設(shè)四邊形APEQ的面積為y（cm2），試探究y的最大值；

（3）當(dāng)t為何值時(shí)，△APQ是等腰三角形．

【考點(diǎn)】S9：相似三角形的判定與性質(zhì)；H7：二次函數(shù)的最值；KH：等腰三角形的性質(zhì)．

【分析】（1）根據(jù)題意以及直角三角形性質(zhì)表達(dá)出CQ、AQ，從而得出結(jié)論，

（2）作PG⊥x軸，將四邊形的面積表示為S△ABC﹣S△BPE﹣S△QCE即可求解，

（3）根據(jù)題意以及三角形相似對(duì)邊比例性質(zhì)即可得出結(jié)論．

【解答】（1）解：AP=2t

∵∠EDF=90°，∠DEF=45°，

∴∠CQE=45°=∠DEF，

∴CQ=CE=t，

∴AQ=8﹣t，

t的取值范圍是：0≤t≤5；

（2）過(guò)點(diǎn)P作PG⊥x軸于G，可求得AB=10，SinB=，PB=10﹣2t，EB=6﹣t，

∴PG=PBSinB=（10﹣2t）

∴y=S△ABC﹣S△PBE﹣S△QCE==

∴當(dāng)（在0≤t≤5內(nèi)），y有最大值，y最大值=（cm2）

（3）若AP=AQ，則有2t=8﹣t解得：（s）

若AP=PQ，如圖①：過(guò)點(diǎn)P作PH⊥AC，則AH=QH=，PH∥BC

∴△APH∽△ABC，

∴，

即，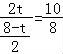

解得：（s）

若AQ=PQ，如圖②：過(guò)點(diǎn)Q作QI⊥AB，則AI=PI=AP=t

∵∠AIQ=∠ACB=90°∠A=∠A，

∴△AQI∽△ABC

∴即，

解得：（s）

綜上所述，當(dāng)或或時(shí)，△APQ是等腰三角形．