由于格式問題此試題可能會出現(xiàn)亂碼的情況

為了方便您閱讀請點擊右上角的全屏查看

2018秦皇島市中考數(shù)學(xué)沖刺試題????????????? ????????????? ????????????? 　????????????? ????????????? ?????????????

一、選擇題????????????? ????????????? ?????????????

1．若二次根式在實數(shù)范圍內(nèi)有意義，則x的取值范圍是（　　）????????????? ????????????? ?????????????

A．x≥2????????????? B．x＞2????????????? C．x＜2????????????? D．x≤2

2．下列各組數(shù)中，不能作為直角三角形邊長的是（　　）????????????? ????????????? ?????????????

A．9，12，15????????????? B．5，12，13????????????? C．1，2，????????????? D．，3，5，7

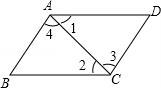
3．如圖，若∠1=∠2，AD=BC，則四邊形ABCD是（　　）????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

A．平行四邊形????????????? B．菱形????????????? ?????????????

C．正方形????????????? D．以上說法都不對????????????? ?????????????

4．若一次函數(shù)y=kx+b的圖象經(jīng)過y軸的正半軸上一點，且y隨x的增大而減小，那么k，b的取值范圍是（　　）????????????? ????????????? ?????????????

A．k＞0，b＞0????????????? B．k＞0，b＜0????????????? C．k＜0，b＞0????????????? D．k＜0，b＜0

5．（秦皇島中考數(shù)學(xué)）對于一組數(shù)據(jù)：3、3、2、3、6、3、10、3、6、3、2，下列說法正確的是（　　）????????????? ????????????? ?????????????

A．這組數(shù)據(jù)的眾數(shù)是3????????????? ????????????? ?????????????

B．這組數(shù)據(jù)的眾數(shù)與中位數(shù)的數(shù)值不等????????????? ????????????? ?????????????

C．這組數(shù)據(jù)的中位數(shù)與平均數(shù)的數(shù)值相等????????????? ????????????? ?????????????

D．這組數(shù)據(jù)的平均數(shù)與眾數(shù)的數(shù)值相等????????????? ????????????? ?????????????

6．某校七年級有13名同學(xué)參加百米競賽，預(yù)賽成績各不相同，要取前6名參加決賽，小梅已經(jīng)知道了自己的成績，她想知道自己能否進入決賽，還需要知道這13名同學(xué)成績的（　　）????????????? ????????????? ?????????????

A．中位數(shù)????????????? B．眾數(shù)????????????? C．平均數(shù)????????????? D．極差

7．已知數(shù)據(jù)x1，x2，…，xn的方差是S21，x1﹣a，x2﹣a，…，xn﹣a的方差是S22，則（　　）????????????? ????????????? ?????????????

A．S21＞S22????????????? B．S21＞S22????????????? ?????????????

C．S21=S22????????????? D．S21與S21無法比較????????????? ?????????????

8．一次函數(shù)y=x圖象向下平移2個單位長度后，對應(yīng)函數(shù)關(guān)系式是（　　）????????????? ????????????? ?????????????

A．y=2x????????????? B．y=x????????????? C．y=x+2????????????? D．y=x﹣2

9．一次函數(shù)y=kx+b，經(jīng)過（1，1），（2，﹣4），則k與b的值為（　　）????????????? ????????????? ?????????????

A．????????????? B．????????????? C．????????????? D．

10．已知△ABC的周長為50cm，中位線DE=8cm，中位線EF=10cm，則另一條中位線DF的長是（　　）????????????? ????????????? ?????????????

A．5cm????????????? B．7cm????????????? C．9cm????????????? D．10cm

11．已知x+y=，xy=，則x2+y2的值為（　　）????????????? ????????????? ?????????????

A．5????????????? B．3????????????? C．2????????????? D．1

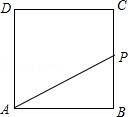
12．如圖，正方形ABCD的邊長為4，P為正方形邊上一動點，沿A→D→C→B→A 的路徑勻速移動，設(shè)P點經(jīng)過的路徑長為x，△APD的面積是y，則下列圖象能大致反映y與x的函數(shù)關(guān)系的是（　　）????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

A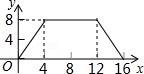．????????????? B．?????????????

C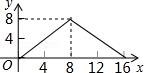．????????????? D．

　????????????? ????????????? ?????????????

二、填空題????????????? ????????????? ?????????????

13．20142015=　　．????????????? ????????????? ?????????????

14（秦皇島中考數(shù)學(xué)）．數(shù)據(jù)3，1，﹣2，5，3的平均數(shù)是　　，中位數(shù)是　　，眾數(shù)是　　．????????????? ????????????? ?????????????

15．某中學(xué)期中考試，八（1）班第一小組10人數(shù)學(xué)考試的成績?yōu)椋?00分3人，90分5人，80分2人，則全組數(shù)學(xué)平均成績?yōu)椤　》郑????????????? ????????????? ?????????????

16．在函數(shù)中，自變量x的取值范圍是　　．????????????? ????????????? ?????????????

17．已知直線y=2x+8與x軸和y軸的交點的坐標分別是　　、　　；與兩條坐標軸圍成的三角形的面積是　　．????????????? ????????????? ?????????????

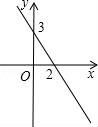
18．如圖，直線y=kx+b（k≠0）與x軸的交點為（2，0），與y軸的交點為（0，3），則關(guān)于x的不等式0＜kx+b＜3的解集是　　．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

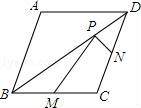
19．已知菱形ABCD的兩條對角線分別為6和8，M、N分別是邊BC、CD的中點，P是對角線BD上一點，則PM+PN的最小值=　　．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

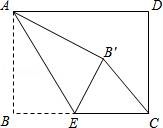
20．如圖，矩形ABCD中，AB=6，BC=8，點E是BC邊上一點，連接AE，把∠B沿AE折疊，使點B落在點B′處，當△CEB′為直角三角形時，BE的長為　　．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

三、解答題????????????? ????????????? ?????????????

21．（秦皇島中考數(shù)學(xué)）為了從甲、乙兩名同學(xué)中選拔一個參加比賽，對他們的射擊水平進行了測驗，兩個在相同條件下各射靶10次，命中的環(huán)數(shù)如下（單位：環(huán)）????????????? ????????????? ?????????????

甲：7，8，6，8，6，5，9，10，7，4????????????? ????????????? ?????????????

乙：9，5，7，8，6，8，7，6，7，7????????????? ????????????? ?????????????

（1）求甲，乙，S甲2，S乙2；????????????? ????????????? ?????????????

（2）你認為該選拔哪名同學(xué)參加射擊比賽？為什么？????????????? ????????????? ?????????????

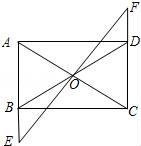
22．如圖，矩形ABCD中，O是AC與BD的交點，過O點的直線EF與AB，CD的延長線分別交于E，F(xiàn)．????????????? ????????????? ?????????????

（1）求證：△BOE≌△DOF；????????????? ????????????? ?????????????

（2）當EF與AC滿足什么關(guān)系時，以A，E，C，F(xiàn)為頂點的四邊形是菱形？證明你的結(jié)論．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

23．已知：如圖，直線y1=x+1經(jīng)過點B（2，n），且與x軸交于點A．????????????? ????????????? ?????????????

（1）求n及點A坐標；????????????? ????????????? ?????????????

（2）若函數(shù)y2=kx（k≠0）的圖象經(jīng)過點B，請畫出這個函數(shù)的圖象，并結(jié)合圖象比較函數(shù)y1與y2的大小關(guān)系．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

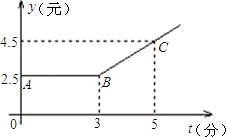
24．如圖，折線ABC是甲地向乙地打長途電話所需要付的電話費y（元）與通話時間t（分鐘）之間關(guān)系的圖象（注意：通話時間不足1分鐘按1分鐘計費）．????????????? ????????????? ?????????????

（1）通話1分鐘，要付電話費多少元？通話5分鐘要付多少電話費？????????????? ????????????? ?????????????

（2）通話多少分鐘內(nèi)，所支付的電話費一樣多？????????????? ????????????? ?????????????

（3）通話3.2分鐘應(yīng)付電話費多少元？????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

25．（秦皇島中考數(shù)學(xué)）抗震救災(zāi)中，某縣糧食局為了保證庫存糧食的安全，決定將甲、乙兩個倉庫的糧食，全部轉(zhuǎn)移到具有較強抗震功能的A、B兩倉庫．已知甲庫有糧食100噸，乙?guī)煊屑Z食80噸，而A庫的容量為70噸，B庫的容量為110噸．從甲、乙兩庫到A、B兩庫的路程和運費如下表：（表中“元/噸千米”表示每噸糧食運送1千米所需人民幣）????????????? ????????????? ?????????????

?????????????

（1）若甲庫運往A庫糧食x噸，請寫出將糧食運往A、B兩庫的總運費y（元）與x（噸）的函數(shù)關(guān)系式；????????????? ????????????? ?????????????

（2）當甲、乙兩庫各運往A、B兩庫多少噸糧食時，總運費最省，最省的總運費是多少？????????????? ????????????? ?????????????

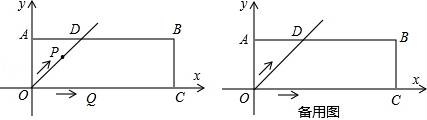
26．在平面直角坐標系xOy中，過原點O及點A（0，2）、C（6，0）作矩形OABC，∠AOC的平分線交AB于點D．點P從點O出發(fā)，以每秒個單位長度的速度沿射線OD方向移動；同時點Q從點O出發(fā)，以每秒2個單位長度的速度沿x軸正方向移動．設(shè)移動時間為t秒．????????????? ????????????? ?????????????

（1）當點P移動到點D時，t=　　秒；?? ????????????? ????????????? ?????????????

（2）連接點A，C，求直線AC的解析式；????????????? ????????????? ?????????????

（3）若點M是直線AC上第一象限內(nèi)一點，是否存在某一時刻，使得四邊形OPMQ為平行四邊形？若存在，請直接寫出t的值及點M的坐標；若不存在，請說明理由．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

2015-2016學(xué)年河北省秦皇島市八年級（下）期末數(shù)學(xué)試卷????????????? ????????????? ?????????????

參考答案與試題解析????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

一、選擇題????????????? ????????????? ?????????????

1．（秦皇島中考數(shù)學(xué)）若二次根式在實數(shù)范圍內(nèi)有意義，則x的取值范圍是（　　）????????????? ????????????? ?????????????

A．x≥2????????????? B．x＞2????????????? C．x＜2????????????? D．x≤2

【考點】二次根式有意義的條件．????????????? ????????????? ?????????????

【分析】由二次根式在實數(shù)范圍內(nèi)有意義，可得2﹣x≥0，繼而求得答案．????????????? ????????????? ?????????????

【解答】解：∵二次根式在實數(shù)范圍內(nèi)有意義，????????????? ????????????? ?????????????

∴2﹣x≥0，????????????? ????????????? ?????????????

解得：x≤2．????????????? ????????????? ?????????????

故選D．????????????? ????????????? ?????????????

【點評】此題考查了二次根式有意義的條件．注意二次根式中的被開方數(shù)必須是非負數(shù)，否則二次根式無意義．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

2．下列各組數(shù)中，不能作為直角三角形邊長的是（　　）????????????? ????????????? ?????????????

A．9，12，15????????????? B．5，12，13????????????? C．1，2，????????????? D．，3，5，7

【考點】勾股定理的逆定理．????????????? ????????????? ?????????????

【分析】根據(jù)勾股定理的逆定理：如果三角形有兩邊的平方和等于第三邊的平方，那么這個三角形是直角三角形．如果沒有這種關(guān)系，這個就不是直角三角形．????????????? ????????????? ?????????????

【解答】解：A、92+122=152，符合勾股定理的逆定理，故本選項不符合題意；????????????? ????????????? ?????????????

B、52+122=132，符合勾股定理的逆定理，故本選項不符合題意；????????????? ????????????? ?????????????

C、12+（）2=22，符合勾股定理的逆定理，故本選項不符合題意；????????????? ????????????? ?????????????

D、32+52≠72，不符合勾股定理的逆定理，故本選項符合題意．????????????? ????????????? ?????????????

故選D．????????????? ????????????? ?????????????

【點評】本題考查了勾股定理的逆定理，在應(yīng)用勾股定理的逆定理時，應(yīng)先認真分析所給邊的大小關(guān)系，確定最大邊后，再驗證兩條較小邊的平方和與最大邊的平方之間的關(guān)系，進而作出判斷．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

3．如圖，若∠1=∠2，AD=BC，則四邊形ABCD是（　　）????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

A．平行四邊形????????????? B．菱形????????????? ?????????????

C．正方形????????????? D．以上說法都不對????????????? ?????????????

【考點】平行四邊形的判定．????????????? ????????????? ?????????????

【分析】根據(jù)題意判斷出△ACD≌△CAB，故可得出∠3=∠4，由此可得出結(jié)論．????????????? ????????????? ?????????????

【解答】解：在△ACD與△CAB中，????????????? ????????????? ?????????????

∵，????????????? ????????????? ?????????????

∴△ACD≌△CAB，????????????? ????????????? ?????????????

∴∠3=∠4，????????????? ????????????? ?????????????

∴AB∥CD，????????????? ????????????? ?????????????

∴四邊形ABCD是平行四邊形．????????????? ????????????? ?????????????

故選A．????????????? ????????????? ?????????????

【點評】本題考查的是平行四邊形的判定，熟知兩組對邊分別平行的四邊形是平行四邊形是解答此題的關(guān)鍵．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

4．（秦皇島中考數(shù)學(xué)）若一次函數(shù)y=kx+b的圖象經(jīng)過y軸的正半軸上一點，且y隨x的增大而減小，那么k，b的取值范圍是（　　）????????????? ????????????? ?????????????

A．k＞0，b＞0????????????? B．k＞0，b＜0????????????? C．k＜0，b＞0????????????? D．k＜0，b＜0

【考點】一次函數(shù)圖象與系數(shù)的關(guān)系．????????????? ????????????? ?????????????

【分析】根據(jù)圖象在坐標平面內(nèi)的位置關(guān)系確定k，b的取值范圍，從而求解．????????????? ????????????? ?????????????

【解答】解：函數(shù)值y隨x的增大而減小，則k＜0；????????????? ????????????? ?????????????

圖象與y軸的正半軸相交，則b＞0．????????????? ????????????? ?????????????

故選C．????????????? ????????????? ?????????????

【點評】函數(shù)值y隨x的增大而減小?k＜0；函數(shù)值y隨x的增大而增大?k＞0；????????????? ????????????? ?????????????

一次函數(shù)y=kx+b圖象與y軸的正半軸相交?b＞0，一次函數(shù)y=kx+b圖象與y軸的負半軸相交?b＜0，一次函數(shù)y=kx+b圖象過原點?b=0．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

5．對于一組數(shù)據(jù)：3、3、2、3、6、3、10、3、6、3、2，下列說法正確的是（　　）????????????? ????????????? ?????????????

A．這組數(shù)據(jù)的眾數(shù)是3????????????? ????????????? ?????????????

B．這組數(shù)據(jù)的眾數(shù)與中位數(shù)的數(shù)值不等????????????? ????????????? ?????????????

C．這組數(shù)據(jù)的中位數(shù)與平均數(shù)的數(shù)值相等????????????? ????????????? ?????????????

D．這組數(shù)據(jù)的平均數(shù)與眾數(shù)的數(shù)值相等????????????? ????????????? ?????????????

【考點】眾數(shù)；加權(quán)平均數(shù)；中位數(shù)．????????????? ????????????? ?????????????

【分析】根據(jù)平均數(shù)、眾數(shù)、中位數(shù)的定義和公式分別對每一項進行分析，再進行判斷即可．????????????? ????????????? ?????????????

【解答】解：數(shù)據(jù)3出現(xiàn)次數(shù)最多，故眾數(shù)為3，????????????? ????????????? ?????????????

故選A．????????????? ????????????? ?????????????

【點評】此題考查了平均數(shù)、眾數(shù)、中位數(shù)的知識，中位數(shù)是將一組數(shù)據(jù)從小到大（或從大到小）重新排列后，最中間的那個數(shù)（最中間兩個數(shù)的平均數(shù)），叫做這組數(shù)據(jù)的中位數(shù)，眾數(shù)是一組數(shù)據(jù)中出現(xiàn)次數(shù)最多的數(shù)．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

6．某校七年級有13名同學(xué)參加百米競賽，預(yù)賽成績各不相同，要取前6名參加決賽，小梅已經(jīng)知道了自己的成績，她想知道自己能否進入決賽，還需要知道這13名同學(xué)成績的（　　）????????????? ????????????? ?????????????

A．中位數(shù)????????????? B．眾數(shù)????????????? C．平均數(shù)????????????? D．極差

【考點】統(tǒng)計量的選擇．????????????? ????????????? ?????????????

【分析】由于有13名同學(xué)參加百米競賽，要取前6名參加決賽，故應(yīng)考慮中位數(shù)的大小．????????????? ????????????? ?????????????

【解答】解：共有13名學(xué)生參加競賽，取前6名，所以小梅需要知道自己的成績是否進入前六．????????????? ????????????? ?????????????

我們把所有同學(xué)的成績按大小順序排列，第7名學(xué)生的成績是這組數(shù)據(jù)的中位數(shù)，????????????? ????????????? ?????????????

所以小梅知道這組數(shù)據(jù)的中位數(shù)，才能知道自己是否進入決賽．????????????? ????????????? ?????????????

故選：A．????????????? ????????????? ?????????????

【點評】本題考查了用中位數(shù)的意義解決實際問題．將一組數(shù)據(jù)按照從小到大（或從大到小）的順序排列，如果數(shù)據(jù)的個數(shù)是奇數(shù)，則處于中間位置的數(shù)就是這組數(shù)據(jù)的中位數(shù)．如果這組數(shù)據(jù)的個數(shù)是偶數(shù)，則中間兩個數(shù)據(jù)的平均數(shù)就是這組數(shù)據(jù)的中位數(shù)．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

7．（秦皇島中考數(shù)學(xué)）已知數(shù)據(jù)x1，x2，…，xn的方差是S21，x1﹣a，x2﹣a，…，xn﹣a的方差是S22，則（　　）????????????? ????????????? ?????????????

A．S21＞S22????????????? B．S21＞S22????????????? ?????????????

C．S21=S22????????????? D．S21與S21無法比較????????????? ?????????????

【考點】方差．????????????? ????????????? ?????????????

【分析】列出二個算式的方差表達式進行對比即可．????????????? ????????????? ?????????????

【解答】解：由題意知，設(shè)原來的數(shù)據(jù)的平均數(shù)為1，每個數(shù)據(jù)都減小了a，則平均數(shù)變?yōu)?img src="http://img.chusan.com/upLoad/doc2017/1u0k80nh/164747.030.jpeg" width="10" height="18" alt="" />1﹣a，原來的方差s12= [（x1﹣）2+（x2﹣）2+…+（xn﹣）2]，現(xiàn)在的方差s22= [（x1+a﹣﹣a）2+（x2+a﹣﹣a）2+…+（xn+a﹣﹣a）2]= [（x1﹣）2+（x2﹣）2+…+（xn﹣）2]，即方差不變．????????????? ????????????? ?????????????

故選C．????????????? ????????????? ?????????????

【點評】本題說明了當一組數(shù)據(jù)的每一個數(shù)都加上（或減去）同一個數(shù)a后，得到的新數(shù)據(jù)的方差不變．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

8．一次函數(shù)y=x圖象向下平移2個單位長度后，對應(yīng)函數(shù)關(guān)系式是（　　）????????????? ????????????? ?????????????

A．y=2x????????????? B．y=x????????????? C．y=x+2????????????? D．y=x﹣2

【考點】一次函數(shù)圖象與幾何變換．????????????? ????????????? ?????????????

【分析】注意平移時k的值不變，只有b發(fā)生變化．????????????? ????????????? ?????????????

【解答】解：原直線的k=1，b=0；向下平移2個單位長度得到了新直線，????????????? ????????????? ?????????????

那么新直線的k=1，b=0﹣2=﹣2．????????????? ????????????? ?????????????

∴新直線的解析式為y=x﹣2．????????????? ????????????? ?????????????

故選D．????????????? ????????????? ?????????????

【點評】本題考查了一次函數(shù)圖象的幾何變換，難度不大，要注意平移后k值不變．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

9．（秦皇島中考數(shù)學(xué)）一次函數(shù)y=kx+b，經(jīng)過（1，1），（2，﹣4），則k與b的值為（　　）????????????? ????????????? ?????????????

A．????????????? B．????????????? C．????????????? D．

【考點】待定系數(shù)法求一次函數(shù)解析式．????????????? ????????????? ?????????????

【分析】由于一次函數(shù)y=kx+b經(jīng)過（1，1），（2，﹣4），應(yīng)用待定系數(shù)法即可求出函數(shù)的解析式．????????????? ????????????? ?????????????

【解答】解：把（1，1），（2，﹣4）代入一次函數(shù)y=kx+b，????????????? ????????????? ?????????????

得，????????????? ????????????? ?????????????

解得：．????????????? ????????????? ?????????????

故選：C．????????????? ????????????? ?????????????

【點評】本題考查用待定系數(shù)法求解函數(shù)解析式，只需把所給的點的坐標代入即可．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

10．已知△ABC的周長為50cm，中位線DE=8cm，中位線EF=10cm，則另一條中位線DF的長是（　　）????????????? ????????????? ?????????????

A．5cm????????????? B．7cm????????????? C．9cm????????????? D．10cm

【考點】三角形中位線定理；平行四邊形的判定．????????????? ????????????? ?????????????

【分析】三角形的中位線等于第三邊的一半，所以三條中位線的長為：50÷2=25，所求的中位線為25減去另兩條中位線的長．????????????? ????????????? ?????????????

【解答】解：另一條中位線DF的長為：50÷2﹣（8+10）=7，故選B．????????????? ????????????? ?????????????

【點評】本題利用了三角形的中位線等于第三邊的一半求解．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

11．已知x+y=，xy=，則x2+y2的值為（　　）????????????? ????????????? ?????????????

A．5????????????? B．3????????????? C．2????????????? D．1

【考點】二次根式的化簡求值．????????????? ????????????? ?????????????

【分析】由（x+y）2=x2+y2+2xy，得出x2+y2=（x+y）2﹣2xy，再帶入已知數(shù)據(jù)求解即可．????????????? ????????????? ?????????????

【解答】解：x2+y2=（x+y）2﹣2xy????????????? ????????????? ?????????????

=（）2﹣2????????????? ????????????? ?????????????

=3+2+2﹣2????????????? ????????????? ?????????????

=5．????????????? ????????????? ?????????????

故選A．????????????? ????????????? ?????????????

【點評】本題考查了二次根式的化簡求值，解答本題的關(guān)鍵在于先對原式進行恰當?shù)幕喨缓蟠肭笾担????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

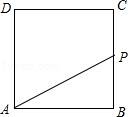
12（秦皇島中考數(shù)學(xué)）．如圖，正方形ABCD的邊長為4，P為正方形邊上一動點，沿A→D→C→B→A 的路徑勻速移動，設(shè)P點經(jīng)過的路徑長為x，△APD的面積是y，則下列圖象能大致反映y與x的函數(shù)關(guān)系的是（　　）????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

A．????????????? B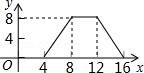．????????????? C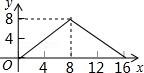．????????????? D．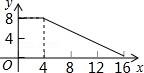

【考點】動點問題的函數(shù)圖象．????????????? ????????????? ?????????????

【分析】根據(jù)動點從點A出發(fā)，首先向點D運動，此時y不隨x的增加而增大，當點P在DC山運動時，y隨著x的增大而增大，當點P在CB上運動時，y不變，據(jù)此作出選擇即可．????????????? ????????????? ?????????????

【解答】解：①當點P由點A向點D運動時，y的值為0；????????????? ????????????? ?????????????

②當點P在DC上運動時，y隨著x的增大而增大；????????????? ????????????? ?????????????

③當點p在CB上運動時，y=ABAD，y不變；????????????? ????????????? ?????????????

④當點P在BA上運動時，y隨x的增大而減小．????????????? ????????????? ?????????????

故選B．????????????? ????????????? ?????????????

【點評】本題考查了動點問題的函數(shù)圖象，解決動點問題的函數(shù)圖象問題關(guān)鍵是發(fā)現(xiàn)y隨x的變化而變化的趨勢．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

二、填空題????????????? ????????????? ?????????????

13．（1﹣）20142015=　1+　．????????????? ????????????? ?????????????

【考點】二次根式的混合運算．????????????? ????????????? ?????????????

【分析】把（1+）2015化成（1+）2014（1+），與（1﹣）2014，利用積的乘方的逆用得：[（1﹣）（1+）]2014=（﹣1）2014=1，最后得出結(jié)果．????????????? ????????????? ?????????????

【解答】解：（1﹣）20142015，????????????? ????????????? ?????????????

=（1﹣）20142014（1+），????????????? ????????????? ?????????????

=[（1﹣）（1+）]2014（1+），????????????? ????????????? ?????????????

=1+．????????????? ????????????? ?????????????

【點評】本題考查了二次根式的混合運算，主要運用了積的乘方的逆用，對高次方進行變形，化成1或﹣1的高次方進行計算，從而得出結(jié)果．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

14．（秦皇島中考數(shù)學(xué)）數(shù)據(jù)3，1，﹣2，5，3的平均數(shù)是　2　，中位數(shù)是　3　，眾數(shù)是　3　．????????????? ????????????? ?????????????

【考點】眾數(shù)；算術(shù)平均數(shù)；中位數(shù)．????????????? ????????????? ?????????????

【分析】先根據(jù)平均數(shù)=求出該組數(shù)據(jù)的平均數(shù)，再將該組數(shù)據(jù)按照從小到大的順序排列，根據(jù)中位數(shù)和眾數(shù)的概念解答即可．????????????? ????????????? ?????????????

【解答】解：平均數(shù)===2，????????????? ????????????? ?????????????

將這組數(shù)據(jù)按照從小到大的順序排列為：﹣2，1，3，3，5，????????????? ????????????? ?????????????

可得出中位數(shù)為：3，眾數(shù)為：3．????????????? ????????????? ?????????????

故答案為：2，3，3．????????????? ????????????? ?????????????

【點評】本題考查了眾數(shù)和中位數(shù)的概念：（1）一組數(shù)據(jù)中出現(xiàn)次數(shù)最多的數(shù)據(jù)叫做眾數(shù)．（2）將一組數(shù)據(jù)按照從小到大（或從大到小）的順序排列，如果數(shù)據(jù)的個數(shù)是奇數(shù)，則處于中間位置的數(shù)就是這組數(shù)據(jù)的中位數(shù)；如果這組數(shù)據(jù)的個數(shù)是偶數(shù)，則中間兩個數(shù)據(jù)的平均數(shù)就是這組數(shù)據(jù)的中位數(shù)．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

15．某中學(xué)期中考試，八（1）班第一小組10人數(shù)學(xué)考試的成績?yōu)椋?00分3人，90分5人，80分2人，則全組數(shù)學(xué)平均成績?yōu)椤?1　分．????????????? ????????????? ?????????????

【考點】加權(quán)平均數(shù)．????????????? ????????????? ?????????????

【分析】首先求出這10人的數(shù)學(xué)總成績?yōu)槎嗌伲蝗缓笄蟪鋈M數(shù)學(xué)平均成績?yōu)槎嗌偌纯桑????????????? ????????????? ?????????????

【解答】解：（100×3+90×5+80×2）÷10????????????? ????????????? ?????????????

=（300+450+160）÷10????????????? ????????????? ?????????????

=910÷10????????????? ????????????? ?????????????

=91（分）????????????? ????????????? ?????????????

答：全組數(shù)學(xué)平均成績?yōu)?1分．????????????? ????????????? ?????????????

故答案為：91．????????????? ????????????? ?????????????

【點評】此題主要考查了平均數(shù)的含義和求法，要熟練掌握．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

16．在函數(shù)中，自變量x的取值范圍是　x≤1且x≠﹣2　．????????????? ????????????? ?????????????

【考點】函數(shù)自變量的取值范圍；分式有意義的條件；二次根式有意義的條件．????????????? ????????????? ?????????????

【分析】根據(jù)二次根式的性質(zhì)和分式的意義，被開方數(shù)大于等于0，分母不等于0，就可以求解．????????????? ????????????? ?????????????

【解答】解：根據(jù)二次根式有意義，分式有意義得：1﹣x≥0且x+2≠0，????????????? ????????????? ?????????????

解得：x≤1且x≠﹣2．????????????? ????????????? ?????????????

故答案為：x≤1且x≠﹣2．????????????? ????????????? ?????????????

【點評】本題考查的知識點為：分式有意義，分母不為0；二次根式的被開方數(shù)是非負數(shù)．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

17．（秦皇島中考數(shù)學(xué)）已知直線y=2x+8與x軸和y軸的交點的坐標分別是　（﹣4，0）　、　（0，8）　；與兩條坐標軸圍成的三角形的面積是　16　．????????????? ????????????? ?????????????

【考點】一次函數(shù)圖象上點的坐標特征．????????????? ????????????? ?????????????

【分析】讓直線解析式的縱坐標為0即可得到與x軸的交點坐標；讓橫坐標為0即可得到與y軸的交點坐標，與兩條坐標軸圍成的三角形的面積應(yīng)等于×x軸上點的橫坐標的絕對值×y軸上點的縱坐標．????????????? ????????????? ?????????????

【解答】解：當y=0時，x=﹣4，????????????? ????????????? ?????????????

∴直線y=2x+8與x軸的交點坐標為（﹣4，0）；????????????? ????????????? ?????????????

當x=0時，y=8，????????????? ????????????? ?????????????

∴直線y=2x+8與y軸的交點坐標為（0，8）；????????????? ????????????? ?????????????

∴三角形的底是|﹣4|，高是8，????????????? ????????????? ?????????????

∴與兩條坐標軸圍成的三角形的面積是×|﹣4|×8=16．????????????? ????????????? ?????????????

故填（﹣4，0）、（0，8）、16．????????????? ????????????? ?????????????

【點評】本題考查的知識點為：一次函數(shù)與y軸的交點的橫坐標為0；一次函數(shù)與x軸的交點的縱坐標為0，在求面積的時候注意坐標與線段的轉(zhuǎn)化．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

18．如圖，直線y=kx+b（k≠0）與x軸的交點為（2，0），與y軸的交點為（0，3），則關(guān)于x的不等式0＜kx+b＜3的解集是　0＜x＜2　．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

【考點】一次函數(shù)與一元一次不等式．????????????? ????????????? ?????????????

【分析】根據(jù)一次函數(shù)的性質(zhì)得出y隨x的增大而增大，當x＜2時，y＜0，即可求出答案．????????????? ????????????? ?????????????

【解答】解：∵直線y=kx+b（k＞0）與x軸的交點為（2，0），與y軸的交點為（0，3），????????????? ????????????? ?????????????

∴y隨x的增大而增大，????????????? ????????????? ?????????????

當x＜2時，y＜0，????????????? ????????????? ?????????????

即kx+b＜0．????????????? ????????????? ?????????????

0＜kx+b＜3的解集為：0＜x＜2，????????????? ????????????? ?????????????

故答案為：0＜x＜2????????????? ????????????? ?????????????

【點評】本題主要考查對一次函數(shù)與一元一次不等式，一次函數(shù)的性質(zhì)等知識點的理解和掌握，能熟練地運用性質(zhì)進行說理是解此題的關(guān)鍵．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

19．已知菱形ABCD的兩條對角線分別為6和8，M、N分別是邊BC、CD的中點，P是對角線BD上一點，則PM+PN的最小值=　5　．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

【考點】軸對稱-最短路線問題；菱形的性質(zhì)．????????????? ????????????? ?????????????

【分析】作M關(guān)于BD的對稱點Q，連接NQ，交BD于P，連接MP，此時MP+NP的值最小，連接AC，求出CP、PB，根據(jù)勾股定理求出BC長，證出MP+NP=QN=BC，即可得出答案．????????????? ????????????? ?????????????

【解答】（秦皇島中考數(shù)學(xué)）解：????????????? ????????????? ?????????????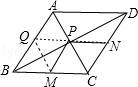

作M關(guān)于BD的對稱點Q，連接NQ，交BD于P，連接MP，此時MP+NP的值最小，連接AC，????????????? ????????????? ?????????????

∵四邊形ABCD是菱形，????????????? ????????????? ?????????????

∴AC⊥BD，∠QBP=∠MBP，????????????? ????????????? ?????????????

即Q在AB上，????????????? ????????????? ?????????????

∵MQ⊥BD，????????????? ????????????? ?????????????

∴AC∥MQ，????????????? ????????????? ?????????????

∵M為BC中點，????????????? ????????????? ?????????????

∴Q為AB中點，????????????? ????????????? ?????????????

∵N為CD中點，四邊形ABCD是菱形，????????????? ????????????? ?????????????

∴BQ∥CD，BQ=CN，????????????? ????????????? ?????????????

∴四邊形BQNC是平行四邊形，????????????? ????????????? ?????????????

∴NQ=BC，????????????? ????????????? ?????????????

∵四邊形ABCD是菱形，????????????? ????????????? ?????????????

∴CP=AC=3，BP=BD=4，????????????? ????????????? ?????????????

在Rt△BPC中，由勾股定理得：BC=5，????????????? ????????????? ?????????????

即NQ=5，????????????? ????????????? ?????????????

∴MP+NP=QP+NP=QN=5，????????????? ????????????? ?????????????

故答案為：5．????????????? ????????????? ?????????????

【點評】本題考查了軸對稱﹣最短路線問題，平行四邊形的性質(zhì)和判定，菱形的性質(zhì)，勾股定理的應(yīng)用，解此題的關(guān)鍵是能根據(jù)軸對稱找出P的位置．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

20．如圖，矩形ABCD中，AB=6，BC=8，點E是BC邊上一點，連接AE，把∠B沿AE折疊，使點B落在點B′處，當△CEB′為直角三角形時，BE的長為　3或6　．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

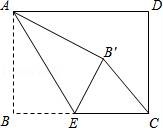【考點】翻折變換（折疊問題）．????????????? ????????????? ?????????????

【分析】當△CEB′為直角三角形時，有兩種情況：????????????? ????????????? ?????????????

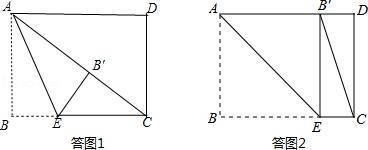
①當點B′落在矩形內(nèi)部時，如答圖1所示．????????????? ????????????? ?????????????

連結(jié)AC，先利用勾股定理計算出AC=10，根據(jù)折疊的性質(zhì)得∠AB′E=∠B=90°，而當△CEB′為直角三角形時，只能得到∠EB′C=90°，所以點A、B′、C共線，即∠B沿AE折疊，使點B落在對角線AC上的點B′處，則EB=EB′，AB=AB′=6，可計算出CB′=4，設(shè)BE=x，則EB′=x，CE=8﹣x，然后在Rt△CEB′中運用勾股定理可計算出x．????????????? ????????????? ?????????????

②當點B′落在AD邊上時，如答圖2所示．此時四邊形ABEB′為正方形．????????????? ????????????? ?????????????

【解答】（秦皇島中考數(shù)學(xué)）解：當△CEB′為直角三角形時，有兩種情況：????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

①當點B′落在矩形內(nèi)部時，如答圖1所示．????????????? ????????????? ?????????????

連結(jié)AC，????????????? ????????????? ?????????????

在Rt△ABC中，AB=6，BC=8，????????????? ????????????? ?????????????

∴AC==10，????????????? ????????????? ?????????????

∵∠B沿AE折疊，使點B落在點B′處，????????????? ????????????? ?????????????

∴∠AB′E=∠B=90°，????????????? ????????????? ?????????????

當△CEB′為直角三角形時，只能得到∠EB′C=90°，????????????? ????????????? ?????????????

∴點A、B′、C共線，即∠B沿AE折疊，使點B落在對角線AC上的點B′處，如圖，????????????? ????????????? ?????????????

∴EB=EB′，AB=AB′=6，????????????? ????????????? ?????????????

∴CB′=10﹣6=4，????????????? ????????????? ?????????????

設(shè)BE=x，則EB′=x，CE=8﹣x，????????????? ????????????? ?????????????

在Rt△CEB′中，????????????? ????????????? ?????????????

∵EB′2+CB′2=CE2，????????????? ????????????? ?????????????

∴x2+42=（8﹣x）2，????????????? ????????????? ?????????????

解得x=3，????????????? ????????????? ?????????????

∴BE=3；????????????? ????????????? ?????????????

②當點B′落在AD邊上時，如答圖2所示．????????????? ????????????? ?????????????

此時ABEB′為正方形，????????????? ????????????? ?????????????

∴BE=AB=6．????????????? ????????????? ?????????????

綜上所述，BE的長為3或6．????????????? ????????????? ?????????????

故答案為：3或6．????????????? ????????????? ?????????????

【點評】本題考查了折疊問題：折疊前后兩圖形全等，即對應(yīng)線段相等；對應(yīng)角相等．也考查了矩形的性質(zhì)以及勾股定理．注意本題有兩種情況，需要分類討論，避免漏解．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

三、（秦皇島中考數(shù)學(xué)）解答題????????????? ????????????? ?????????????

21．為了從甲、乙兩名同學(xué)中選拔一個參加比賽，對他們的射擊水平進行了測驗，兩個在相同條件下各射靶10次，命中的環(huán)數(shù)如下（單位：環(huán)）????????????? ????????????? ?????????????

甲：7，8，6，8，6，5，9，10，7，4????????????? ????????????? ?????????????

乙：9，5，7，8，6，8，7，6，7，7????????????? ????????????? ?????????????

（1）求甲，乙，S甲2，S乙2；????????????? ????????????? ?????????????

（2）你認為該選拔哪名同學(xué)參加射擊比賽？為什么？????????????? ????????????? ?????????????

【考點】方差．????????????? ????????????? ?????????????

【分析】（1）根據(jù)平均數(shù)的計算公式先求出平均數(shù)，再根據(jù)方差公式進行計算即可；????????????? ????????????? ?????????????

（2）根據(jù)方差的意義，方差越小越穩(wěn)定，即可得出答案．????????????? ????????????? ?????????????

【解答】解：（1）甲=（7+8+6+8+6+5+9+10+7+4）÷10=7；????????????? ????????????? ?????????????

乙=（9+5+7+8+6+8+7+6+7+7）÷10=7；????????????? ????????????? ?????????????

S甲2= [2（7﹣7）2+2（8﹣7）2+2（6﹣7）2+（5﹣7）2+（9﹣7）2+（10﹣7）2+（4﹣7）2]=3；????????????? ????????????? ?????????????

S乙2= [4（7﹣7）2+2（8﹣7）2+2（6﹣7）2+（5﹣7）2+（9﹣7）2]=1.2；????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

（2）∵甲=乙，S甲2＞S乙2，????????????? ????????????? ?????????????

∴乙較穩(wěn)定，????????????? ????????????? ?????????????

∴該選拔乙同學(xué)參加射擊比賽．????????????? ????????????? ?????????????

【點評】本題考查方差的定義：一般地設(shè)n個數(shù)據(jù)，x1，x2，…xn的平均數(shù)為，則方差S2= [（x1﹣）2+（x2﹣）2+…+（xn﹣）2]，它反映了一組數(shù)據(jù)的波動大小，方差越大，波動性越大，反之也成立．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

22．如圖，矩形ABCD中，O是AC與BD的交點，過O點的直線EF與AB，CD的延長線分別交于E，F(xiàn)．????????????? ????????????? ?????????????

（1）求證：△BOE≌△DOF；????????????? ????????????? ?????????????

（2）當EF與AC滿足什么關(guān)系時，以A，E，C，F(xiàn)為頂點的四邊形是菱形？證明你的結(jié)論．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

【考點】菱形的判定；全等三角形的判定；矩形的性質(zhì)．????????????? ????????????? ?????????????

【分析】（秦皇島中考數(shù)學(xué)）（1）由矩形的性質(zhì)：OB=OD，AE∥CF證得△BOE≌△DOF；????????????? ????????????? ?????????????

（2）若四邊形EBFD是菱形，則對角線互相垂直，因而可添加條件：EF⊥AC，????????????? ????????????? ?????????????

當EF⊥AC時，∠EOA=∠FOC=90°，????????????? ????????????? ?????????????

∵AE∥FC，????????????? ????????????? ?????????????

∴∠EAO=∠FCO，矩形對角線的交點為O，????????????? ????????????? ?????????????

∴OA=OC，????????????? ????????????? ?????????????

∴△AOE≌△COF，????????????? ????????????? ?????????????

∴OE=OF，根據(jù)對角線互相垂直平分的四邊形是菱形．????????????? ????????????? ?????????????

∴四邊形EBFD是菱形．????????????? ????????????? ?????????????

【解答】（1）證明：∵四邊形ABCD是矩形，????????????? ????????????? ?????????????

∴OB=OD（矩形的對角線互相平分），????????????? ????????????? ?????????????

AE∥CF（矩形的對邊平行）．????????????? ????????????? ?????????????

∴∠E=∠F，∠OBE=∠ODF．????????????? ????????????? ?????????????

∴△BOE≌△DOF（AAS）．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

（2）解：當EF⊥AC時，四邊形AECF是菱形．????????????? ????????????? ?????????????

證明：∵四邊形ABCD是矩形，????????????? ????????????? ?????????????

∴OA=OC（矩形的對角線互相平分）．????????????? ????????????? ?????????????

又∵由（1）△BOE≌△DOF得，OE=OF，????????????? ????????????? ?????????????

∴四邊形AECF是平行四邊形（對角線互相平分的四邊形是平行四邊形）????????????? ????????????? ?????????????

又∵EF⊥AC，????????????? ????????????? ?????????????

∴四邊形AECF是菱形（對角線互相垂直的平行四邊形是菱形）．????????????? ????????????? ?????????????

【點評】本題利用了：1、矩形的性質(zhì)，2、全等三角形的判定和性質(zhì)，3、菱形的判定．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

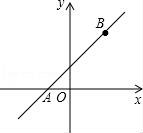
23．已知：如圖，直線y1=x+1經(jīng)過點B（2，n），且與x軸交于點A．????????????? ????????????? ?????????????

（1）求n及點A坐標；????????????? ????????????? ?????????????

（2）若函數(shù)y2=kx（k≠0）的圖象經(jīng)過點B，請畫出這個函數(shù)的圖象，并結(jié)合圖象比較函數(shù)y1與y2的大小關(guān)系．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

【考點】一次函數(shù)圖象上點的坐標特征；正比例函數(shù)的圖象．????????????? ????????????? ?????????????

【分析】（1）把B點代入y1=x+1可求得n的值，可求得函數(shù)解析式，再令y=0，可求得A點坐標；????????????? ????????????? ?????????????

（2）把B點坐標代入y2=kx可求得k的值，可求得解析式，利用兩點法可畫出其圖象，再結(jié)合圖象可比較y1與y2的大小關(guān)系．????????????? ????????????? ?????????????

【解答】（秦皇島中考數(shù)學(xué)）解：????????????? ????????????? ?????????????

（1）把點B坐標代入y1=x+1中，可得n=2+1=3，????????????? ????????????? ?????????????

當y=0時，x+1=0，解得x=﹣1，????????????? ????????????? ?????????????

∴A點坐標為（﹣1，0）；????????????? ????????????? ?????????????

（2）由（1）可知B點坐標為（2，3），????????????? ????????????? ?????????????

把B點坐標代入y2=kx可得3=2k，解k=，????????????? ????????????? ?????????????

∴y2=x，其圖象為過原點的直線，????????????? ????????????? ?????????????

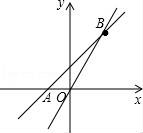
函數(shù)y2=x圖象如圖所示，????????????? ????????????? ?????????????

當x=2時，y1=y2，????????????? ????????????? ?????????????

當x＞2時，y1＜y2，????????????? ????????????? ?????????????

當x＜2時，y1＞y2．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

【點評】本題主要考查函數(shù)圖象的交點問題，掌握函數(shù)圖象上點的坐標滿足函數(shù)解析式是解題的關(guān)鍵．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

24．如圖，折線ABC是甲地向乙地打長途電話所需要付的電話費y（元）與通話時間t（分鐘）之間關(guān)系的圖象（注意：通話時間不足1分鐘按1分鐘計費）．????????????? ????????????? ?????????????

（1）通話1分鐘，要付電話費多少元？通話5分鐘要付多少電話費？????????????? ????????????? ?????????????

（2）通話多少分鐘內(nèi)，所支付的電話費一樣多？????????????? ????????????? ?????????????

（3）通話3.2分鐘應(yīng)付電話費多少元？????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

【考點】一次函數(shù)的應(yīng)用．????????????? ????????????? ?????????????

【分析】（1）觀察圖象，可知當0＜t≤3時，y=2.5，得出t=1時對應(yīng)的y值；C點的縱坐標的值即為通話5分鐘時要付的電話費；????????????? ????????????? ?????????????

（2）此段時間內(nèi)所付電話費不因為時間而改變，即圖象與橫軸平行，得出結(jié)果；????????????? ????????????? ?????????????

（3）當t≥3時，y是t的一次函數(shù)，用待定系數(shù)法求出解析式，把t=4代入，求出答案．????????????? ????????????? ?????????????

【解答】（秦皇島中考數(shù)學(xué)）解：（1）根據(jù)圖象可知，通話1分鐘時，要付電話費2.5元，通話5分鐘時，要付費4.5元；????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

（2）根據(jù)圖象可知，通話3分鐘內(nèi)，所支付的電話費一樣多；????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

（3）當t＞3時，設(shè)y=kt+b????????????? ????????????? ?????????????

把B（3，2.5），C（5，4.5）代入????????????? ????????????? ?????????????

得????????????? ????????????? ?????????????

解得，????????????? ????????????? ?????????????

y=t﹣0.5????????????? ????????????? ?????????????

當T=3.2時，y=4﹣0.5=3.5，????????????? ????????????? ?????????????

故當t=3.2分鐘時，電話費是3.5元．????????????? ????????????? ?????????????

【點評】此題比較復(fù)雜，關(guān)鍵是正確理解題意，然后分析圖形要分清不同時間段，電話費的不同找出函數(shù)關(guān)系式進行解答．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

25．抗震救災(zāi)中，某縣糧食局為了保證庫存糧食的安全，決定將甲、乙兩個倉庫的糧食，全部轉(zhuǎn)移到具有較強抗震功能的A、B兩倉庫．已知甲庫有糧食100噸，乙?guī)煊屑Z食80噸，而A庫的容量為70噸，B庫的容量為110噸．從甲、乙兩庫到A、B兩庫的路程和運費如下表：（表中“元/噸千米”表示每噸糧食運送1千米所需人民幣）????????????? ????????????? ?????????????

?????????????

（1）若甲庫運往A庫糧食x噸，請寫出將糧食運往A、B兩庫的總運費y（元）與x（噸）的函數(shù)關(guān)系式；????????????? ????????????? ?????????????

（2）當甲、乙兩庫各運往A、B兩庫多少噸糧食時，總運費最省，最省的總運費是多少？????????????? ????????????? ?????????????

【考點】一次函數(shù)的應(yīng)用．????????????? ????????????? ?????????????

【分析】弄清調(diào)動方向，再依據(jù)路程和運費列出y（元）與x（噸）的函數(shù)關(guān)系式，最后可以利用一次函數(shù)的增減性確定“最省的總運費”．????????????? ????????????? ?????????????

【解答】解：（1）依題意有：若甲庫運往A庫糧食x噸，則甲庫運到B庫（100﹣x）噸，乙?guī)爝\往A庫（70﹣x）噸，乙?guī)爝\到B庫（10+x）噸．????????????? ????????????? ?????????????

則，解得：0≤x≤70．????????????? ????????????? ?????????????

y=12×20x+10×25（100﹣x）+12×15（70﹣x）+8×20×[110﹣（100﹣x）]????????????? ????????????? ?????????????

=﹣30x+39200????????????? ????????????? ?????????????

其中0≤x≤70????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

（2）（秦皇島中考數(shù)學(xué)）上述一次函數(shù)中k=﹣30＜0????????????? ????????????? ?????????????

∴y隨x的增大而減小????????????? ????????????? ?????????????

∴當x=70噸時，總運費最省????????????? ????????????? ?????????????

最省的總運費為：﹣30×70+39200=37100（元）????????????? ????????????? ?????????????

答：從甲庫運往A庫70噸糧食，往B庫運送30噸糧食，從乙?guī)爝\往A庫0噸糧食，從乙?guī)爝\往B庫80噸糧食時，總運費最省為37100元．????????????? ????????????? ?????????????

【點評】本題是一次函數(shù)與不等式的綜合題，先解不等式確定自變量的取值范圍，然后依據(jù)一次函數(shù)的增減性來確定“最佳方案”．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????

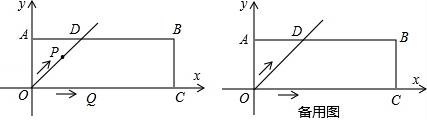
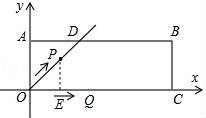
26．在平面直角坐標系xOy中，過原點O及點A（0，2）、C（6，0）作矩形OABC，∠AOC的平分線交AB于點D．點P從點O出發(fā)，以每秒個單位長度的速度沿射線OD方向移動；同時點Q從點O出發(fā)，以每秒2個單位長度的速度沿x軸正方向移動．設(shè)移動時間為t秒．????????????? ????????????? ?????????????

（1）當點P移動到點D時，t=　2　秒；?? ????????????? ????????????? ?????????????

（2）連接點A，C，求直線AC的解析式；????????????? ????????????? ?????????????

（3）若點M是直線AC上第一象限內(nèi)一點，是否存在某一時刻，使得四邊形OPMQ為平行四邊形？若存在，請直接寫出t的值及點M的坐標；若不存在，請說明理由．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

【考點】一次函數(shù)綜合題．????????????? ????????????? ?????????????

【分析】（1）根據(jù)矩形以及角平分線的性質(zhì)可得出△OAD為等腰直角三角形，再根據(jù)點A的坐標結(jié)合等腰直角三角形的性質(zhì)即可得出OD的長度，從而可得出t值；????????????? ????????????? ?????????????

（2）設(shè)直線AC解析式為y=kx+b，根據(jù)點A、C的坐標利于待定系數(shù)法即可求出直線AC的解析式；????????????? ????????????? ?????????????

（3）假設(shè)存在，找出點P、O、Q三點的坐標，根據(jù)平行四邊形的性質(zhì)﹣﹣對角線互相平分，分別以O(shè)P、OQ、PQ為對角線求出點M的坐標，再根據(jù)點M是直線AC上第一象限內(nèi)一點，即可求出t值以及點M的坐標．????????????? ????????????? ?????????????

【解答】（秦皇島中考數(shù)學(xué)）解：（1）∵四邊形OABC為矩形，且∠AOC的平分線交AB于點D，????????????? ????????????? ?????????????

∴△OAD為等腰直角三角形，????????????? ????????????? ?????????????

∵點A（0，2），????????????? ????????????? ?????????????

∴OA=2，OD=2，????????????? ????????????? ?????????????

點P移動到點D時，t=2÷=2（秒）．????????????? ????????????? ?????????????

故答案為：2．????????????? ????????????? ?????????????

（2）設(shè)直線AC解析式為y=kx+b，????????????? ????????????? ?????????????

將點A（0，2）、C（6，0）代入y=kx+b中，????????????? ????????????? ?????????????

得：，解得：，????????????? ????????????? ?????????????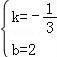

∴直線AC解析式為y=﹣x+2．????????????? ????????????? ?????????????

（3）假設(shè)存在，過點P作PE⊥x軸于點E，如圖所示．????????????? ????????????? ?????????????

由（1）可知△POE為等腰直角三角形，????????????? ????????????? ?????????????

∴點P（t，t）．????????????? ????????????? ?????????????

O（0，0），Q（2t，0）．????????????? ????????????? ?????????????

四邊形OPMQ為平行四邊形分三種情況：????????????? ????????????? ?????????????

①以O(shè)P為對角線時，點M（0+t﹣2t，0+t﹣0），即（﹣t，t），????????????? ????????????? ?????????????

∵點M在第一象限，????????????? ????????????? ?????????????

∴此情況不符合要求；????????????? ????????????? ?????????????

②以O(shè)Q為對角線時，點M（0+2t﹣t，0+0﹣t），即（t，﹣t），????????????? ????????????? ?????????????

∵點M在第一象限，????????????? ????????????? ?????????????

∴此情況不符合要求；????????????? ????????????? ?????????????

③以PQ為對角線時，點M（t+2t﹣0，t+0﹣0），即（3t，t），????????????? ????????????? ?????????????

∵點M在第一象限內(nèi)，且點M在直線AC上，????????????? ????????????? ?????????????

∴t=﹣×3t+2，解得：t=1，????????????? ????????????? ?????????????

此時點M的坐標為（3，1）．????????????? ????????????? ?????????????

綜上可知：若點M是直線AC上第一象限內(nèi)一點，存在某一時刻，使得四邊形OPMQ為平行四邊形，此時t=1，點M的坐標為（3，1）．????????????? ????????????? ?????????????

????????????? ????????????? ?????????????

【點評】本題考查了矩形的性質(zhì)、等腰直角三角形的性質(zhì)、待定系數(shù)法求函數(shù)解析式以及平行四邊形的性質(zhì)，解題的關(guān)鍵是：（1）求出線段OD的長；（2）利用待定系數(shù)法求出函數(shù)解析式；（3）分三種情況討論．本題屬于中檔題，難度不大，解決該題型題目時，根據(jù)平行四邊形的性質(zhì)﹣﹣對角線互相平分，由平行四邊形的三個頂點坐標求出第四個頂點的坐標是關(guān)鍵．????????????? ????????????? ?????????????

　????????????? ????????????? ?????????????