此試題可能存在亂碼情況，在查看時請點(diǎn)擊右上角全屏查看

2018年周口中考數(shù)學(xué)模擬試題

注意事項(xiàng)：

1．本試卷共6頁，三個大題，滿分120分，考試時間100分鐘．

2．請用黑色水筆把答案直接寫在答題卡上，寫在試題卷上的答案無效．

一、選擇題 （每小題3分，共24分）

下列各小題均有四個答案，其中只有一個是正確的，將正確答案的代號字母

涂在答題卡上．

1．的倒數(shù)是　????????????????????????????????????????????????????

A．?? B．??? C． ????????????? ???? D．2?

2．估計(jì)的值在哪兩個數(shù)之間　??????????????????????????????????????

A．1與2??? B． 2 與3 C．3與4?? D．4與5?

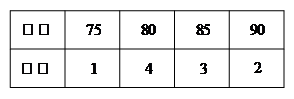3．有10位同學(xué)參加數(shù)學(xué)競賽，成績?nèi)缦卤恚?/p>

 

 

 

 

 

 

 

則上列數(shù)據(jù)中的中位數(shù)是????????????????????????????????????????????

A． 80??? B． 82.5??? C． 85??? D． 87.5

4．我國計(jì)劃在2020年左右發(fā)射火星探測衛(wèi)星，據(jù)科學(xué)研究測量，火星距離地球的最近距離約為5500萬千米，這個數(shù)據(jù)用科學(xué)計(jì)數(shù)法表示為??????????????????????

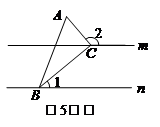A．5.5×106?? B．????????????? 5.5×107??? C．55×107?? D．0.55×108?

5．如圖，直線m∥n，△ABC的頂點(diǎn)B，C分別在n，m上，

且∠C ＝ 90°，若∠1＝ 40° ，則∠2的度數(shù)為?????????????????????????????????????????????????????

A．????????????? 130°?? B．120°? C．110°? D．100°

 

6．如圖所示是某個幾何體的三視圖，該幾何體是?????????????????????????

A． 圓錐?? B．三棱錐????????????? ? C．圓柱? D．三棱柱

 

 

 

 

 

 

 

 

 

 

 

 

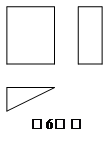
7．關(guān)于x的一元二次方程有

兩個不相等的實(shí)數(shù)根，則m的取值范圍是?? 　????????????????????????????????????????????

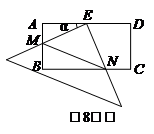A．m ≥ B．m ≤ C．m ＜ D．m ＞

8．在矩形ABCD中，AD = 2AB = 4，E為AD的中點(diǎn)，一塊

足夠大的三角板的直角頂點(diǎn)與E重合，將三角板繞點(diǎn)E

旋轉(zhuǎn)，三角板的兩直角邊分別交AB、BC（或它們的延長線）

于點(diǎn)M、N，設(shè)∠AEM? = α（0°＜α ＜ 90°），給出四個結(jié)論：

①AM ＝CN????? ②∠AME ＝∠BNE??? ③BN－AM ＝2??? ④

上述結(jié)論中正確的個數(shù)是

A．1?? B．2?? C．3?? D．4

二、填空題（ 每小題3分，共21分）

9．化簡：的結(jié)果是　　　　　　．

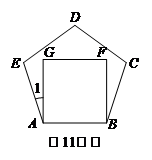10．化簡：6（7＋1）（72＋1）（74＋1）（78＋1）（716＋1）＋1＝　　　　　　．

11．有一個正五邊形和一個正方形邊長相等，如圖放置，

則∠1＝　　　　　　．

12．二次函數(shù)y＝x2－2x＋3的圖象向左平移一個單位，

再向上平移兩個單位后，所得二次函數(shù)的解析式

為　　　　　???????? 　．

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

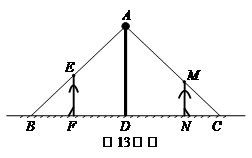
13．如圖，小強(qiáng)和小華共同站在路燈下，

小強(qiáng)的身高EF＝1.8m，小華的身高

MN＝1.5m，他們的影子恰巧等于自

己的身高，即BF＝1.8m，CN＝1.5m，

且兩人相距4.7m，則路燈AD的高度是　　　．

14．如圖，在△ABC中，AB＝AC，∠A＝36°，且BC＝2，則AB ＝??????????? ．

15．如圖，在平面直角坐標(biāo)系中，函數(shù)y＝2x和y＝－ x的圖象分別為直線l1，l2，過

點(diǎn)（1，0）作x軸的垂線交l1于點(diǎn)A1，過點(diǎn)A1作y軸的垂線交l2于點(diǎn)A2，過點(diǎn)A2

作x軸的垂線交l1于點(diǎn)A3，過點(diǎn)A3作y軸的垂線交l2于點(diǎn)A4，…，依次進(jìn)行下去，

則點(diǎn)A2017的坐標(biāo)為　　　　　?????? 　．

 

 

 

 

 

 

 

 

 

 

 

 

 

 

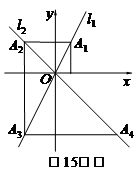
三、解答題：（本大題共8個小題，滿分75分）

16．（8分）先化簡，再求值：

÷，其中x＝2sin30°＋2cos45°．

 

 

 

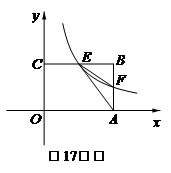
17．（9分）如圖，在矩形OABC中，OA＝3，OC＝2，

F是AB上的一個動點(diǎn)（F不A、B與重合），過點(diǎn)

F的反比例函數(shù)y＝的圖象與邊BC交于點(diǎn)E．

（1）當(dāng)F為AB的中點(diǎn)時，求該函數(shù)的解析式；

（2）當(dāng)k為何值時，△EFA的面積最大，最大面

積是多少？

 

 

 

 

18．（9分）在甲、乙兩名同學(xué)中選拔一人參加“中國詩詞大會”，在相同的測試條件下，兩人5次測試成績（單位：分）如下：

????? ???? 甲：79，86，82，85，83

?????????? 乙：88，79，90，81，72

回答下列問題：

（1）甲成績的平均數(shù)是?????????? ，乙成績的平均數(shù)是?????????? ；

（2）經(jīng)計(jì)算可知：S2甲＝6，S2乙＝42，你認(rèn)為選誰參加競賽比較合適，說明理由；

?? （3）如果從兩個人5次的成績中各隨機(jī)抽取一次進(jìn)行分析，求抽到的兩個人的成績都大于80分的概率．

 

 

 

19．（9分）如圖，AB為⊙O的直徑，F(xiàn)為弦AC的中點(diǎn)，連接OF并延長交弧AC于點(diǎn)D，過點(diǎn)D作⊙O的切線，交BA的延長線于點(diǎn)E．

（1）求證：AC∥DE；

（2）連接CD，若OA＝AE＝2時，

求出四邊形ACDE的面積．

 

 

 

 

20．（9分）南沙群島是我國的固有領(lǐng)土，現(xiàn)在我南海漁民要

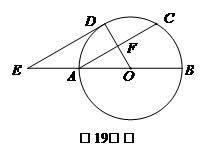
在南沙群島某海島附近進(jìn)行捕魚作業(yè)，當(dāng)漁船航行至B

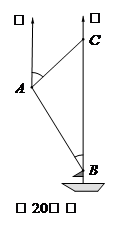處時，測得該島位于正北方向20（1＋）海里的C處，

為防止某國的巡警干擾，就請求我A處的魚監(jiān)船前往C

處護(hù)航，已知C位于A處的北偏東45°方向上，A位于

B的北偏西30°的方向上，求A、C之間的距離．

 

 

 

 

 

 

 

 

 

 

 

 

 

 

21．（10分）某學(xué)校是乒乓球體育傳統(tǒng)項(xiàng)目學(xué)校，為進(jìn)一步推動該項(xiàng)目的開展，學(xué)校準(zhǔn)備到體育用品商店購買直握球拍和橫握球拍若干副，并且每買一副球拍必須要買10個乒乓球，乒乓球的單價(jià)為2元/個，若購買20副直握球拍和15副橫握球拍共花費(fèi)9000元；購買10副橫握球拍比購買5副直握球拍多花費(fèi)1600元．

（1）求兩種球拍每副多少元？

（2）若學(xué)校購買兩種球拍共40副，且直握球拍數(shù)量不多于橫握球拍的3倍，請你給出一種費(fèi)用最少的方案，并求出該方案所需費(fèi)用．

 

 

 

 

 

 

 

 

 

22．（10分）如圖（1），在正方形ABCD中，點(diǎn)E、F分別是邊BC，AB上的點(diǎn)，且CE＝BF，連接DE，過點(diǎn)E作EG⊥DE，使EG＝DE，連接FG，F(xiàn)C．

（1）請判斷：FG與CE的數(shù)量關(guān)系是????????? ，位置關(guān)系是???????????? ；

（2）如圖（2），若點(diǎn)E，F(xiàn)分別是CB，BA的延長線上的點(diǎn)，其它條件不變，（1）中的結(jié)論是否仍然成立？請作出判斷并給出證明；

（3）如圖（3）若點(diǎn)E，F(xiàn)分別是BC，AB延長線上的點(diǎn)，其它條件不變，（1）中的結(jié)論是否仍然成立？請直接寫出你的判斷．

 

 

 

 

 

 

 

 

 

 

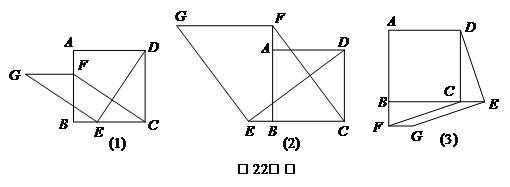
23．（11分）如圖，在平面直角坐標(biāo)系中，直線y＝－2x＋10與x軸，y軸相交于A，B

兩點(diǎn)，點(diǎn)C的坐標(biāo)為（8，4），連接AC，BC．

??? （1）求過O，A，C三點(diǎn)的拋物線的解析式，并判斷△ABC的形狀；

??? （2）動點(diǎn)P從O點(diǎn)出發(fā)，沿OB以每秒兩個單位長度的速度向點(diǎn)B運(yùn)動，同時動

點(diǎn)Q從點(diǎn)B出發(fā)，沿BC以每秒一個單位長度的速度向點(diǎn)C運(yùn)動，規(guī)定其中一個

動點(diǎn)到達(dá)端點(diǎn)時另一個動點(diǎn)也隨之停止運(yùn)動，設(shè)運(yùn)動時間為t秒，當(dāng)t為何值時，

PA＝QA？；

??? （3）在拋物線的對稱軸上，是否存在點(diǎn)M，使A，B，M為頂點(diǎn)的三角形是等腰三

角形？若存在，直接寫出M點(diǎn)的坐標(biāo)；若不存在，請說明理由．

 

???

 

 

 

 

 

 

 

 

　　　　

2018年周口中考數(shù)學(xué)模擬試題參考答案

選擇題（每題3分? 共24分）

題號	1	2	3	4	5	6	7	8
答案	C	C	B	B	A	D	D	C

填空題

9．　10．　　11．18°　12．y＝x2＋4　13．4m　　14．　

15．（，）

三、解答題

16．解：原式=÷??????? ……………………3分

=×

=????????????????????????????? ……………………5分

∵x＝2sin30°＋2cos45°

＝2×＋2×＝3，??????????? ……………………7分

∴原式=．????????????????? ……………………8分

17．解：（1）∵四邊形OABC是矩形，∴AB＝OC＝2，又∵F是AB的中點(diǎn)，

∴AF＝1，∴F（3，1），∴k＝3×1＝3，

∴反比例函數(shù)的解析式為y＝????????????????? ……………………4分

（2）解：∵E（，2），F(xiàn)（3，），

? ∴S△EFA＝AF×BE＝××（3－）＝－k2＋k

＝－（k－3）2＋，∴當(dāng)k＝3時，△EFA的面積最大，

最大面積是 ．?????? ……………………9分

 

18．解：（1）甲成績的平均數(shù)是??? 83?? ，

乙成績的平均數(shù)是?? 82??? ；?????????? ……………………2分

（2）因?yàn)榧椎钠骄煽兇笥谝业钠骄煽儯壹椎姆讲钚∮谝业姆讲睿f明甲的成績更穩(wěn)定，因此，選甲參加競賽更合適；????????????????? ……………………4分

? （3）列表如下：

 

 

 

 

 

 

 

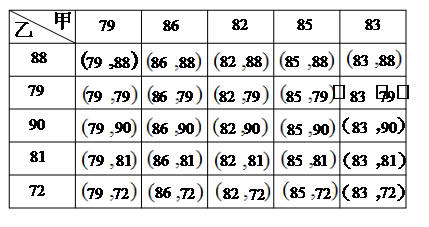
設(shè)抽到的兩個人的成績都大于80分的概率為P

則P＝???????????????????????????????? ……………………9分

19．證明：（1）∵F為弦AC（非直徑）的中點(diǎn)，∴AF＝CF，∴OD⊥AC，

∵DE切⊙O于點(diǎn)D，∴OD⊥DE，∴AC∥DE． ……………………3分

（2）∵AC∥DE，且OA＝AE，∴F為OD的中點(diǎn)，即OF＝FD，又∵AF＝CF，

∠AFO＝∠CFD，∴△AFO≌△CFD（SAS），∴S△AFO＝S△CFD，∴S四邊形ACDE＝S△ODE

在Rt△ODE中，OD＝OA＝AE＝2，∴OE＝4，∴DE＝＝2

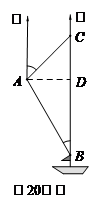
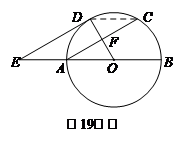∴S四邊形ACDE＝S△ODE＝×OD×OE＝×2×2＝2．?? ……………………9分

 

 

 

 

 

20．解：作AD⊥BC于D，設(shè)AD＝x，依題意可知∠ABC＝30°，

∠ACB＝45°，在Rt△ADC中，CD＝AD＝x，在Rt△ADB中

∵＝tan30°，∴BD＝AD＝x，∵BC＝CD＋BD＝x＋x＝20（1＋），

即x＋x＝20（1＋），

解之得x＝20，∴AC＝AD＝20．

∴A、C之間的距離為20海里．? ……………………9分

21．解：（1）設(shè)直握球拍每副x元，橫握球拍每副y元，依題意可得：

???????? ……………………3分

 

解得：???????????????????????????? ……………………5分

∴直握球拍每副220元，橫握球拍每副260元；

（2）設(shè)購買直握球拍m副，則購買橫握球拍（40－m）副 ，

則，m≤3（40－m），解之得：m≤30 ?????????? ……………………7分

設(shè)購買兩種球拍的總費(fèi)用為W元，則

W＝（220＋2×10）m＋（260＋2×10）（40－m）

? ＝－40 m＋11200

∵－40＜0，∴W隨 m的增大而減小，∴ m取最大值30時，W最小，此時40－m＝10

即學(xué)校購買直握球拍30副，購買橫握球拍10副時，費(fèi)用最少，

W＝－40 m＋11200＝－40×30＋11200＝10000，

∴最少費(fèi)用為10000元．?????????????????????? ……………………10分

22．（1）FG與CE的數(shù)量關(guān)系是FG＝CE，

位置關(guān)系是FG∥CE；?????? ……………………2分

?? （2）（1）中結(jié)論仍然成立，

??? 證明：CE＝BF，∠ABC＝∠ECD＝90°，BC＝CD，

∴△ECD≌△FBC（SAS），∴ED＝FC，∠DEC＝∠CFB，……………………5分

又∵EG＝DE，∴EG＝FC，又∵AB∥CD，

∴∠CFB＝∠FCD，∴∠DEC＝∠FCD，∵∠DEC＋∠EDC＝90°，

∠FCD＋∠EDC＝90°，即∠CMD＝90°，即ED⊥FC，又EG⊥DE，

∴EG∥FC，又EG＝FC，∴四邊形CEGF為平行四邊形，

∴FG＝CE，F(xiàn)G∥CE；?????????????????????? ……………………9分

（3）（1）中結(jié)論仍然成立．??????????????????? ……………………10分

 

 

 

 

 

 

 

23．解：（1）在y＝－2x＋10中，當(dāng)x＝0時，y＝10，y＝0時，x＝5，∴A（5，0），

B（0，10），∵拋物線經(jīng)過O（0，0），故設(shè)過O，A，C三點(diǎn)的拋物線的解析式

為y＝ax2＋bx（a ≠ 0），

則，解得：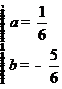

∴過O，A，C三點(diǎn)的拋物線的解析式為y＝x2－x，……………………2分

??? ∵BA2＝102＋52＝125，BC2＝82＋62＝100，AC2＝32＋42＝25，

∴AC2＋BC2＝BA2，即△ABC為直角三角形，且∠ACB＝90°；……………………3分

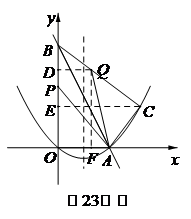?? （2）作CE⊥y軸于E點(diǎn)，QD⊥y軸于D點(diǎn)，QF⊥x軸于點(diǎn)F，

△BEC中，BE︰EC︰BC＝6︰8︰10＝3︰4︰5，∵CE⊥y軸，QD⊥y軸，

∴QD∥ CE ，∴△BDQ ∽△BEC，

∴BD︰DQ︰BQ＝BE︰EC︰BC＝3︰4︰5，

∵BQ＝t，∴BD＝t，DQ＝t，

∴QA2＝QF2＋FA2＝（10－t）2＋（5－t）2＝t2－20t＋125

PA2＝（2t）2＋52＝4t2＋25，若PA＝QA，則PA2＝QA2，

∴4t2＋25＝t2－20t＋125，∴3t2＋20t－100＝0，

解之得：t1＝，t2＝－10，∵0≤t≤5，∴t＝

∴當(dāng)t＝秒時，PA＝QA；……………………7分

（3）存在滿足條件的點(diǎn)M．

M1（，），M2（，－），

M3（，），M4（，）．……………………11分