2018年上海中考數(shù)學(xué)壓軸試卷【精選word版】

由于格式問題，部分試題會(huì)存在亂碼的現(xiàn)象，請(qǐng)考生點(diǎn)擊全屏查看！

一、選擇題（本大題共6題，每題4分，滿分24分）

1、點(diǎn)和⊙都在同一平面內(nèi)，⊙的半徑是3，，則點(diǎn)與⊙的位置是（? ）

A、點(diǎn)在⊙內(nèi)?? B、點(diǎn)在⊙上?? C、點(diǎn)在⊙外?? D、不能確定

2、直角三角形的兩條直角邊的長(zhǎng)分別是3和4，則這個(gè)直角三角形外接圓的半徑是（? ）

A、???? B、???? C、???? D、

3、如圖，某中學(xué)繪制了學(xué)生選擇棋類、武術(shù)、攝影、航模四門校本課程情況的扇形統(tǒng)計(jì)圖，從該圖中可以看出選擇航模的學(xué)生占（? ）

A、18%
B、17%
C、16%
D、15%

4、如果兩圓的半徑分別為2和3，圓心距為6，那么這兩個(gè)圓的位置關(guān)系是（? ）

A、外離??? B、相交??? C、外切??? D、內(nèi)切

5、下列說(shuō)法不正確的是（? ）

A、不在同一直線上的三點(diǎn)確定一個(gè)圓
B、平分弧的直徑垂直平分弧所對(duì)的弦
C、平分弦的直徑垂直于弦
D、在同圓中，如果兩條弦所對(duì)的圓心角相等，那么兩條弦所對(duì)的弧也相等

6、下列正多邊形中，中心角等于內(nèi)角的是（? ）

A、正六邊形?? B、正五邊形??? C、正四邊形??? D、正三邊形

二、填空題（本大題共12題，每題4分，滿分48分）

7、已知圓的半徑長(zhǎng)為，一條弦的長(zhǎng)為，那么這條弦的弦心距等于______

8、已知⊙的直徑為，如果圓心到直線的距離為，那么直線與⊙有______個(gè)公共點(diǎn)

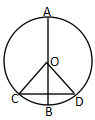
9、如圖，和是⊙的直徑，，若，則的度數(shù)是_____

10、正八邊形的中心角等于______度

11、已知，數(shù)據(jù)的平均數(shù)為12，那么數(shù)據(jù)的平均數(shù)為______

12、數(shù)據(jù)的方差為______

13、已知數(shù)據(jù)的中位數(shù)是3，那么=_____（寫出一個(gè)符合條件的數(shù)）

14、若兩圓相切，半徑分別為和，則兩圓的圓心距的長(zhǎng)為______

15、已知⊙和⊙相切，⊙的半徑長(zhǎng)為，，那么⊙的半徑長(zhǎng)等于_______

16、若正六邊形的邊長(zhǎng)為2，則此正六邊形的邊心距為______

17、要使正五邊形繞著它的中心旋轉(zhuǎn)后能與它本身重合，至少要旋轉(zhuǎn)______度

18、已知⊙的半徑為5，兩條平行弦的長(zhǎng)分別為6和8，那么這兩條弦之間的距離為______

三、解答題（本大題共7題，滿分78分）

19、（本題滿分10分）如圖，已知是⊙的直徑，是弦，且，如果半徑是，，求的長(zhǎng)

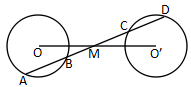
20、（本題滿分10分）如圖，等圓⊙與⊙外離，為的中點(diǎn)，直線過點(diǎn)，交⊙與⊙于點(diǎn)。求證：

21、（本題滿分10分）今年3月5日，某中學(xué)組織六、七年級(jí)200位學(xué)生參與了“走出校門，服務(wù)社會(huì)”的活。該校某數(shù)學(xué)學(xué)習(xí)小組的同學(xué)對(duì)那天參與打掃街道、敬老院服務(wù)和社區(qū)文藝演出的三組人數(shù)進(jìn)行分別統(tǒng)計(jì)，部分?jǐn)?shù)據(jù)如圖所示。（1）參與社區(qū)文藝演出的學(xué)生人數(shù)是_____人，參與敬老院服務(wù)的學(xué)生是_____人；（2）該數(shù)學(xué)學(xué)習(xí)小組的同學(xué)還發(fā)現(xiàn)，六、七年級(jí)參與打掃街道的學(xué)生人數(shù)分別比參與敬老院服務(wù)的學(xué)生人數(shù)多了40%和60%。求參與敬老院服務(wù)的六、七年級(jí)學(xué)生分別有多少人？

22、（本題滿分10分）某校為了了解八年級(jí)學(xué)生（共350人）的身體素質(zhì)情況，體育老師對(duì)八（1）班的50位學(xué)生進(jìn)行一分鐘跳繩次數(shù)測(cè)試，以測(cè)試數(shù)據(jù)為樣本，繪制出部分頻數(shù)分布表和部分頻數(shù)分布直方圖，如下所示

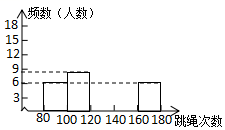
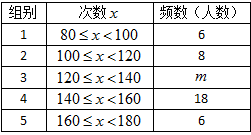
請(qǐng)結(jié)合圖表完成下列問題：

（1）表中的=____

（2）請(qǐng)把頻數(shù)分布直方圖補(bǔ)充完整

（3）這個(gè)樣本數(shù)據(jù)的中位數(shù)落在第_____組

（4）若八年級(jí)學(xué)生一分鐘跳繩次數(shù)（）合格要求是，則估計(jì)八年級(jí)學(xué)生中一分鐘跳繩成績(jī)不合格的約幾人？（要有解題過程）

23、（本題滿分10分）如圖，已知是⊙中的弦，且，分別是的中點(diǎn)，求證：

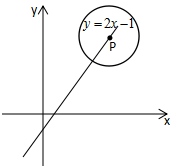
24、（本體滿分12分）如圖，已知⊙的圓心在直線上運(yùn)動(dòng)

（1）若⊙半徑為2，當(dāng)⊙和軸相切時(shí)，求點(diǎn)的坐標(biāo)

（2）若⊙半徑為2，當(dāng)⊙和軸相切時(shí)，求點(diǎn)的坐標(biāo)

（3）若要讓⊙與軸、軸都相切時(shí)，則⊙的半徑是多少？

25、（本題滿分14分）如圖，在中，，，，點(diǎn)是邊上一點(diǎn)，，點(diǎn)是邊上一點(diǎn)，以點(diǎn)為圓心，為半徑作圓，經(jīng)過點(diǎn)，點(diǎn)是邊上一動(dòng)點(diǎn)（點(diǎn)不與重合），作，交射線于點(diǎn)

（1）用直尺圓規(guī)做出圓心，并求圓的半徑長(zhǎng)（保留作圖痕跡）

（2）當(dāng)點(diǎn)的邊上時(shí)，設(shè)，，求關(guān)于的函數(shù)解析式，并寫出它的定義域

（3）聯(lián)結(jié)，當(dāng)與相似時(shí)，推理判斷以點(diǎn)為圓心，為半徑的圓與圓可能產(chǎn)生的各種位置關(guān)系