2018無錫中考數(shù)學試卷
選擇題:(本大題共10小題,每小題3分 共30分)
1.下列等式正確的是( A )
A.![]() =3???? B.
=3???? B.![]() ?? C.
?? C.![]() ?? D.
?? D.![]()
2.函數(shù)![]() 中自變量x的取值范圍是(? B? )
中自變量x的取值范圍是(? B? )
A.![]() ??? B.
??? B.![]() ?? C.
?? C.![]() ???? D.
???? D.![]()
3.下列運算正確的是( D ? )
A.![]() ??? B.
??? B.![]() ??? C.
??? C.![]() ??? D.
??? D.![]()
4.下面每個圖形都是由6個邊長相同的正方形拼成的圖形,其中能折疊成正方體的是(?? C? )
A.![]() B.
B.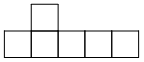 C.
C.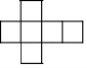 D.
D.
5.下列圖形中的五邊形ABCDE都是正五邊形,則這些圖形中的軸對稱圖形有(? D ? )
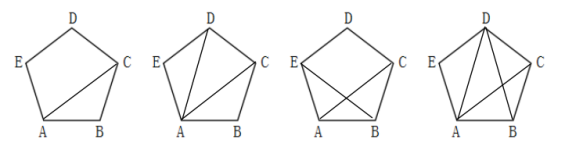
A.1個?? B.2個??? C.3個??? D.4個
已知點P(a,m)、Q(b,n)都在反比例函數(shù)![]() 的圖像上,且a<0<b,則下列結(jié)論一定成立的是( D?? )
的圖像上,且a<0<b,則下列結(jié)論一定成立的是( D?? )
m+n<0?????? B.m+n>0??? C.m<n???? D.m>n
某商場為了解產(chǎn)品A的銷售情況,在上個月的銷售記錄中,隨機抽取了5天A產(chǎn)品的銷售記錄,其售價x(元/件)與對應(yīng)的銷售量y(件)的全部數(shù)據(jù)如下表:
售價x(元/件) | 90 | 95 | 100 | 105 | 110 |
銷量y(件) | 110 | 100 | 80 | 60 | 50 |
則這5天中,A產(chǎn)品平均每件的售價為(? C?? )
A.100元?? B.95元??? C.98元??? D.97.5元
如圖,矩形ABCD中,G是BC中點,過A、D、G三點的圓![]() 與邊AB、CD分別交于點E、點F,給出下列說法:(1)AC與BD的交點是圓
與邊AB、CD分別交于點E、點F,給出下列說法:(1)AC與BD的交點是圓![]() 的圓心;(2)AF與DE的交點是圓
的圓心;(2)AF與DE的交點是圓![]() 的圓心;BC與圓
的圓心;BC與圓![]() 相切。其中正確的說法的個數(shù)是(? C? )
相切。其中正確的說法的個數(shù)是(? C? )
A.0????? B.1???? C.2????? D.3
如圖,已知點E是矩形ABCD的對角線AC上一動點,正方形EFGH的頂點G、H都在邊AD上,若AB=3,BC=4,則tan∠AFE的值(? A? )
等于![]() ?? B.等于
?? B.等于![]() ??? C.等于
??? C.等于![]() ?? D.隨點E位置的變化而變化
?? D.隨點E位置的變化而變化
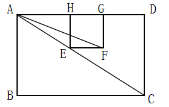
【解答】
![]() EF∥AD
EF∥AD
∴∠AFE=∠FAG
![]() △AEH∽△ACD
△AEH∽△ACD
∴![]()
設(shè)EH=3x,AH=4x
∴HG=GF=3x
∴tan∠AFE=tan∠FAG=![]() =
=![]()
如圖是一個沿![]() 正方形格紙的對角線AB剪下的圖形,一質(zhì)點P由A點出發(fā),沿格點線每次向右或向上運動1個單位長度,則點P由A點運動到B點的不同路徑共有( B ? )
正方形格紙的對角線AB剪下的圖形,一質(zhì)點P由A點出發(fā),沿格點線每次向右或向上運動1個單位長度,則點P由A點運動到B點的不同路徑共有( B ? )
A.4條?? B.5條?? C.6條??? D.7條

【解答】
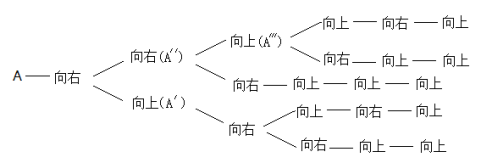

∴有5條路徑,選B
二、填空題(本大題共8小題,每小題2分,共16分)
-2的 相反數(shù)的值等于??? ? .
【解答】2
12、今年“五一”節(jié)日期間,我市四個旅游景區(qū)共接待游客約303 000多人次,這個數(shù)據(jù)用科學記數(shù)法可記為?????? .
【解答】![]()
13、方程![]() 的解是?? ?? .
的解是?? ?? .
【解答】![]()
![]() 的解是?? ?? .
的解是?? ?? .
【解答】![]()
命題“四邊相等的四邊形是菱形”的逆命題是?????? ? ???? .
【解答】 菱形的四邊相等
16、如圖,點A、B、C都在圓O上,OC⊥OB,點A在劣弧![]() 上,且OA=AB,則∠ABC=???? ? ? .
上,且OA=AB,則∠ABC=???? ? ? .
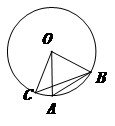
【解答】15°
17.已知△ABC中,AB=10,AC=![]() ,∠B=30°,則△ABC的面積等于???????? .
,∠B=30°,則△ABC的面積等于???????? .
【解答】![]() 或
或![]() ?
?
18、如圖,已知∠XOY=60°,點A在邊OX上,OA=2,過點A作AC⊥OY于點C,以AC為一邊在∠XOY內(nèi)作等邊三角形ABC,點P是△ABC圍成的區(qū)域(包括各邊)內(nèi)的一點,過點P作PD//OY交OX于點D,作PE//OX交OY于點E,設(shè)OD=a,OE=b,則a+2b的取值范圍是??? ? ? .
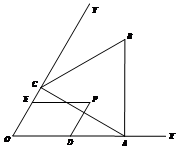
【解答】過P作PH⊥OY交于點H,易證EH=![]()
∴a+2b=![]()
當P在AC邊上時,H與C重合,此時![]() ,
,![]()
當P在點B時,![]() ,
,![]()
∴![]()

19、(本題滿分8分)計算:
(1)![]() ;????????????????? (2)
;????????????????? (2)![]()
【解答】 (1)11??
???????? (2)![]()
20、(本題滿分8分)
分解因式:![]() ???????? (2)解不等式:
???????? (2)解不等式:
【解答】(1)![]()
??????? (2)-2<![]() ≤2
≤2
21、(本題滿分8分)
如圖,平行四邊形ABCD中,E、F分別是邊BC、AD的中點,求證:∠ABF=∠CDE
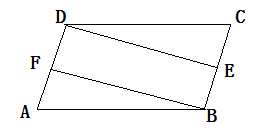
【解答】
![]() ABCD為平行四邊形 AD=AB,CE=AF,∠C=∠A
ABCD為平行四邊形 AD=AB,CE=AF,∠C=∠A
易證△ABF≌△CDE(SAS)
?????? ![]() ∠ABF=∠CDE
∠ABF=∠CDE
22、(本題滿分6分)
某汽車交易市場為了解二手轎車的交易情況,將本市去年成交的二手轎車的全部數(shù)據(jù),以二手轎車交易前的使用時間為標準分為A、B、C、D、E五類,并根據(jù)這些數(shù)據(jù)由甲、乙令人分別繪制了下面的兩幅統(tǒng)計圖(圖都不完整)
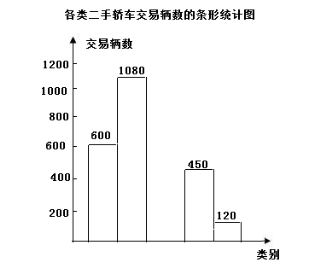
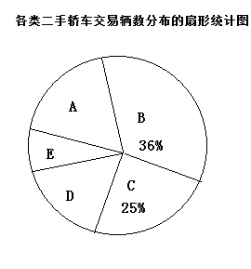
請根據(jù)以上信息,解答下列問題:
該汽車交易市場去年共交易二手車? 3000??? 輛
把這幅條形統(tǒng)計圖補充完整。(畫圖后請標注相應(yīng)的數(shù)據(jù))
在扇形統(tǒng)計圖中,D類二手轎車交易輛數(shù)所對應(yīng)扇形的圓心角為? 54? 度
【解答】

23、某校組織一項公益知識競賽,比賽規(guī)定:每個班級由2名男生、2名女生及1名班主任老師組成代表隊。但參賽時,每班只能有3名隊員上場參賽,班主任老師必須參加,另外2名隊員分別在2名男生和2名女生中各隨機抽出1名。初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任組成了代表隊,求恰好抽到由男生甲、女生丙和這位班主任一起上場參賽的概率。(請用“畫樹狀圖”或“列表”或“列舉”等方法給出分析過程)
【解答】? ![]()
方法一:
? 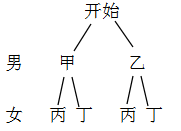
總共的個數(shù)是4,符合條件的個數(shù)是1
![]()
![]()
方法二:
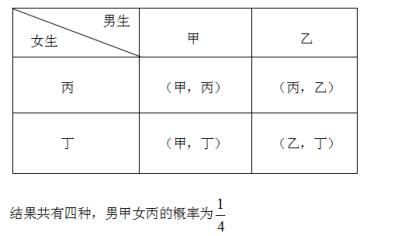
24、(本題滿分8分)
如圖,四邊形ABCD內(nèi)接于圓心O,AB=17,CD=10,∠A=90°,cos B=![]() ,求AD的長。
,求AD的長。
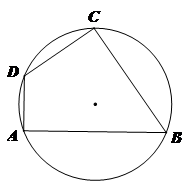
【解答】
![]() DA⊥AB
DA⊥AB
![]() ∠DAB=90°
∠DAB=90°
![]() 在圓O中
在圓O中
![]() ∠DCB=90°
∠DCB=90°
延長AD、BC交于點E,易證∠B=∠EDC
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
在△EAB中,EA=![]()
![]() DA=EA-ED=
DA=EA-ED=![]() =6
=6
25、(本題滿分8分)
一水果店是A酒店某種水果的唯一供貨商,水果店根據(jù)該酒店以往每月的需求情況,本月初專門為他們準備了2600kg的這種水果,已知水果店每售出1kg該水果可獲利潤10元,未售出的部分每1kg將虧損6元。以x(單位:kg,![]() )表示A酒店本月對這種水果的需求量,y(元)表示水果店銷售這批水果所獲得的利潤。
)表示A酒店本月對這種水果的需求量,y(元)表示水果店銷售這批水果所獲得的利潤。
求y關(guān)于x的函數(shù)表達式;
問:當A酒店本月對這種水果的需求量如何時,該水果店銷售這批水果所獲的利潤不少于22000元?
【解答】解:(1)當![]() 時,y=10x-6(2600-x)=16x-15600
時,y=10x-6(2600-x)=16x-15600
當![]() 時,y=2600×10=26000
時,y=2600×10=26000
∴y=![]()
①當![]() 時y=16x-15600≥22000
時y=16x-15600≥22000
???????????????????????? x≥2350∴2350≤x≤2600
???? ②當![]() 時,y=26000>22000,成立
時,y=26000>22000,成立
綜上所述:2350≤x≤3000不少于22000
26、(本題滿分10分)
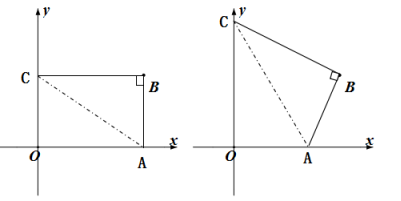
如圖,平面直角坐標系中,已知點B的坐標為(6,4)
(1)請用直尺(不帶刻度)和圓規(guī)作一條直線AC,它與x軸和y軸的正半軸分別交于點A和點C,且使∠ABC=90°,△ABC與△AOC的面積相等。(作圖不必寫作法,但要保留作圖痕跡。)
(2)問:(1)中這樣的直線AC是否唯一?若唯一,請說明理由;若不唯一,請在圖中畫出所有這樣的直線AC,并寫出與之對應(yīng)的函數(shù)表達式。

【解答】解:(1)過B作BA⊥x軸,過B作BC⊥y軸
(2)不唯一,∵![]() ,設(shè)A(a,0)
,設(shè)A(a,0)
∴OA=BA??? a=![]() ? a=
? a=![]()
∴A(![]() ,0)
,0)
設(shè)C(0,c)
∴CO=CB, c=![]() ? c=
? c=![]()
∴C(0,![]() )
)
![]() 或
或![]()
27、(本題滿分10分)
如圖,矩形ABCD中,AB=m,BC=n,將此矩形繞點B順時針方向旋轉(zhuǎn)θ(0°<θ<90°)的到矩形A1BC1D1,點A1在邊CD上,
若m=2,n=1,求在旋轉(zhuǎn)過程中,點D到點D1所經(jīng)過路徑的長度;
將矩形A1BC1D1繼續(xù)繞點B順時針方向旋轉(zhuǎn)得到矩形A2BC2D2,點D2在BC的延長線上,設(shè)邊A2B與CD交于點E,若![]() ,求
,求![]() 的值。
的值。
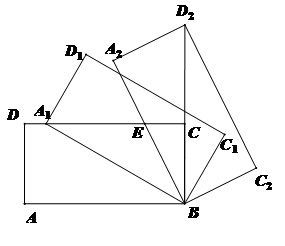
【解答】(1)作A1H⊥AB,
?????????? 且得Sin∠A1BH=1/2
???????? ∴∠A1BH=30°,∴∠DBD1=30°
?????? ∴點D的運動軌跡為![]()
(2)易證△BCE∽△BA2D2
? ∴![]() =
=![]()
∴CE=![]()

AC=![]()
∴? BH=AC=![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
![]()
設(shè)![]()
t=6![]()
解得t=![]()
∴![]()
已知;如圖,一次函數(shù)![]() 的圖象經(jīng)過點A(
的圖象經(jīng)過點A(![]() ,m)(m>0),與y軸交于點B,點C,在線段AB上,且BC=2AC,過點C作
,m)(m>0),與y軸交于點B,點C,在線段AB上,且BC=2AC,過點C作![]() 軸的垂線,垂足為點D,若AC=CD,
軸的垂線,垂足為點D,若AC=CD,
求這個一次函數(shù)的表達式;
已知一開口向下,以直線CD為對稱軸的拋物線經(jīng)過點A,它的頂點為P,若過點P且垂直于AP的直線與![]() 軸的交點為Q(
軸的交點為Q(![]() ,0)求這條拋物線的函數(shù)表達式。
,0)求這條拋物線的函數(shù)表達式。
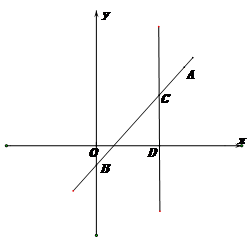
【解答】作BE⊥CD,AF⊥BE,AM⊥CD
易證△BEC∽△BFA?
∴![]()
∵BC=2AC,A(![]() ,m)
,m)
![]()
∴BE=2![]()
C(2![]() ,2
,2![]() k-1)
k-1)
又∵![]()
易得AC=![]()
∵AC=CD,∴![]() =2
=2![]() k-1
k-1
所以得到k=![]()
設(shè)![]() ? A(
? A(![]() ,5)
,5)
?? h×(h-5)=(![]() )×
)×![]()
h =7??
![]() ?
?
5a+7=5?? a=![]() ? 即
? 即![]()

孔乙己是貧困潦倒的知識分子。在書中,孔乙己是一個知識分子,滿口“之乎者也”,但是他很窮,還竊書,說過“讀書人的事,怎么能叫竊,”被人嘲笑,他...

自然界產(chǎn)生氧氣的化學方程式:光合作用的反應(yīng)式為6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反應(yīng)和暗反應(yīng)兩個過程。需要具備光...

有的高校沒有條件,只要學業(yè)水平成績都合格就可以,比如中國科學院大學。有的需要平常學習考試成績,比如北京外國語大學要求高三第一學期期末成績在全...

在四則運算中,表示計算順序,在小括號之后、大括號之前;表示兩個整數(shù)的最小公倍數(shù);表示取未知數(shù)的整數(shù)部分;在函數(shù)中,表示函數(shù)的閉區(qū)間;在線性代...

濟南開設(shè)的最好的職高學校有:濟南方信集團職業(yè)高中、濟南公共交通職業(yè)高中。濟南市公共交通職業(yè)高級中學是由濟南市公共交通總公司承辦,業(yè)務(wù)屬濟南市...

實然:是說事物實際上就是這樣的,但不同于現(xiàn)實性(現(xiàn)實性指其有合理性和客觀性);應(yīng)然:就是應(yīng)該是怎么樣的意思,比如說這件事,就應(yīng)該是那樣的結(jié)果...

地中海氣候一種夏季炎熱干燥、冬季溫和多雨,雨熱不同期的氣候類型。地中海氣候冬季受西風帶控制,鋒面氣旋頻繁活動,氣候溫和,最冷月的氣溫在4-1...

堿石灰,又稱鈉石灰,堿石灰是白色或米黃色粉末,疏松多孔,是氧化鈣(CaO,大約75%),水(H?O,大約20%),氫氧化鈉(NaOH,大約3...