一、選擇題：本大題共10小題，每題3分，共30分．

1．第24屆冬季奧林匹克運(yùn)動(dòng)會(huì)，將于2022年02月04日～2022年02月20日在中華人民共和國北京市和張家口市聯(lián)合舉行．在會(huì)徽的圖案設(shè)計(jì)中，設(shè)計(jì)者常常利用對(duì)稱性進(jìn)行設(shè)計(jì)，下列四個(gè)圖案是歷屆會(huì)徽?qǐng)D案上的一部份圖形，其中不是軸對(duì)稱圖形的是（　　）

A．?????????????

B．?????????????

C．?????????????

D．

2．下列各式運(yùn)算中結(jié)果是a6是（　　）

A．a(chǎn)3+a3?????????????

B．（a3）3?????????????

C．a(chǎn)12÷a2?????????????

D．a(chǎn)3?a3

3．下列各式由左邊到右邊的變形中，是因式分解的是（　　）

A．x3﹣xy2＝x（x﹣y）2?????????????

B．（x+2）（x﹣2）＝x2﹣4?????????????

C．﹣2x2﹣2xy＝﹣2x（x+y）?????????????

D．x2+2x+1＝x（x+2）+1

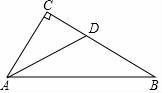
4．如圖，在△ABC中，∠C＝90°，AD是∠BAC的角平分線，若CD＝2，AB＝8，則△ABD的面積是（　　）

A．6?????????????

B．8?????????????

C．10?????????????

D．12

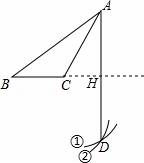
5．如圖，已知鈍角△ABC，依下列步驟尺規(guī)作圖，并保留作圖痕跡．

步驟1：以C為圓心，CA為半徑畫弧①；

步驟2：以B為圓心，BA為半徑畫弧②，交弧①于點(diǎn)D；

步驟3：連接AD，交BC延長線于點(diǎn)H．

下列敘述正確的是（　　）

BH垂直平分線段AD?????????????

B．AC平分∠BAD?????????????

S△ABC＝BC?AH?????????????

D．AB＝AD

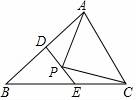
6．如圖，△ABC中，D、E兩點(diǎn)分別在AC、BC上，則AB＝AC，CD＝DE．若∠A＝40°，∠ABD：∠DBC＝3：4，則∠BDE＝（　　）

A．25°?????????????

B．30°?????????????

C．35°?????????????

D．40°

7．多項(xiàng)式x2﹣mxy+9y2能用完全平方因式分解，則m的值是（　　）

A．3?????????????

B．6?????????????

C.±3?????????????

D．±6

8．若a，b，c是三角形的三邊，則代數(shù)式（a﹣b）2﹣c2的值是（　　）

A．正數(shù)?????????????

B．負(fù)數(shù)?????????????

C．等于零?????????????

D．不能確定

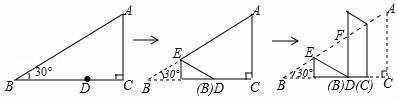
9．如圖，在三角形紙片ABC中，∠C＝90°，∠B＝30°，點(diǎn)D（不與B，C重合）是BC上任意一點(diǎn)，將此三角形紙片按下列方式折疊，若EF的長度為a，則△DEF的周長為（　　）

A．2a?????????????

B．2.5a?????????????

C．3a?????????????

D．4a

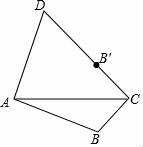
10．如圖，四邊形ABCD中，AB＝AD，點(diǎn)B關(guān)于AC的對(duì)稱點(diǎn)B'恰好落在CD上，若∠BAD＝α，則∠ACB的度數(shù)為（　　）

A．45°?????????????

B.α﹣45°?????????????

C.2分之1α?????????????

D.90°﹣2分之1α

二、填空題：本大題共7小題，每題4分，共28分．把你的答案填入答題紙中相應(yīng)的位置上．

11．（4分）點(diǎn)P（2，﹣3）關(guān)于x軸的對(duì)稱點(diǎn)坐標(biāo)為（　?? 　）．

12．（4分）等腰三角形的一個(gè)內(nèi)角為100°，這個(gè)等腰三角形底角的度數(shù)為(　?? 　)．

13．（4分）已知xm＝4，xn＝3，則xm+n的值為(　?? 　)．

14．（4分）若（2x﹣1）0無意義，則代數(shù)式（4x2﹣1）2008的值為(　?? 　)．

15．（4分）如圖，在△ABC中，AB＝AC，D，E，F(xiàn)分別在BC，AC，AB上的點(diǎn)，且BF＝CD，BD＝CE，∠FDE＝α，則∠A的度數(shù)是(　?? 　)度．（用含α的代數(shù)式表示）

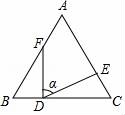
16．（4分）如圖，在△ABC中，AC＝6，BC＝8，AB的垂直平分線DE交AB邊于點(diǎn)D，交BC邊于點(diǎn)E，在線段DE上有一動(dòng)點(diǎn)P，連接AP、PC，則△APC的周長最小值為(　?? 　)．

17．（4分）已知（a﹣2018）2+（2019﹣a）2＝5，則（a﹣2018）（2019﹣a）＝(　?? 　)．

三、解答題：本大題共9小題，共62分．

18．（12分）計(jì)算下列各題：

（1）3x?6x2y

（2）（a+2b）（a﹣2b）

（3）a?a5﹣（a2）3﹣（﹣2a3）2

（4）[x（x2y2﹣xy）﹣y（x2﹣x3y）]÷3x2y．

19．（9分）把下列各式分解因式：

（1）a2b+ab2

（2）ab2﹣4ab+4a

（3）x2（a﹣b）+y2（b﹣a）

20．如圖，點(diǎn)E，F(xiàn)在BC上，BE＝CF，AB＝DC，∠B＝∠C，AF與DE相交于點(diǎn)O，請(qǐng)判斷△OEF的形狀，并說明理由．

21．先化簡，再求值：（x+3）（x﹣3）+（2x﹣1）2﹣4x（x﹣1），其中x＝．

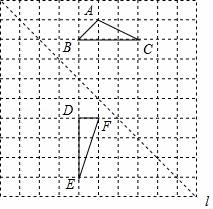
22．（4分）如圖，在邊長為1個(gè)單位長度的小正方形組成的網(wǎng)格中，給出了格點(diǎn)△ABC和△DEF（頂點(diǎn)為網(wǎng)格線的交點(diǎn)），以及過格點(diǎn)的直線l．

（1）將△ABC向右平移兩個(gè)單位長度，再向下平移兩個(gè)單位長度，畫出平移后的三角形．

（2）畫出△DEF關(guān)于直線l對(duì)稱的三角形．

（3）填空：∠C+∠E＝(　?? 　)．

23．已知：線段AB．

（1）尺規(guī)作圖：作線段AB的垂直平分線l，與線段AB交于點(diǎn)D；（保留作圖痕跡，不寫作法）

（2）在（1）的基礎(chǔ)上，點(diǎn)C為l上一個(gè)動(dòng)點(diǎn)（點(diǎn)C不與點(diǎn)D重合），連接CB，過點(diǎn)A作AE⊥BC，垂足為點(diǎn)E．

①當(dāng)垂足E在線段BC上時(shí)，直接寫出∠ABC度數(shù)的取值范圍．

②請(qǐng)你畫出一個(gè)垂足E在線段BC延長線上時(shí)的圖形，并求證∠BAE＝∠BCD．

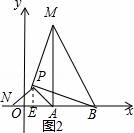
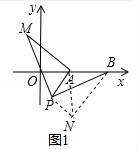
24．（6分）對(duì)于一個(gè)圖形，通過兩種不同的方法計(jì)算它的面積，可以得到一個(gè)數(shù)學(xué)等式，例如圖1可以得到（a+b）2＝a2+2ab+b2，請(qǐng)解答下列問題：

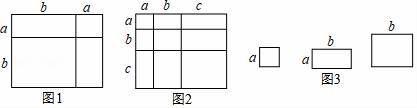
（1）寫出圖2中所表示的數(shù)學(xué)等式(　?? 　)．

（2）根據(jù)整式乘法的運(yùn)算法則，通過計(jì)算驗(yàn)證上述等式．

（3）利用（1）中得到的結(jié)論，解決下面的問題：

若a+b+c＝10，ab+ac+bc＝35，則a2+b2+c2＝(　?? 　)．

（4）小明同學(xué)用圖3中x張邊長為a的正方形，y張邊長為b的正方形z張邊長分別為a、b的長方形紙片拼出一個(gè)面積為（5a+7b）（9a+4b）長方形，則x+y+z＝(　?? 　)．

25．（7分）定義：如圖1，在△ABC和△ADE中，AB＝AC＝AD＝AE，當(dāng)∠BAC+∠DAE＝180°時(shí)，我們稱△ABC與△DAE互為“頂補(bǔ)等腰三角形”，△ABC的邊BC上的高線AM叫做△ADE的“頂心距”，點(diǎn)A叫做“旋補(bǔ)中心”．

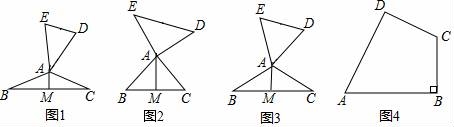
（1）特例感知：在圖2，圖3中，△ABC與△DAE互為“頂補(bǔ)等腰三角形”，AM是“頂心距”．

①如圖2，當(dāng)∠BAC＝90°時(shí)，AM與DE之間的數(shù)量關(guān)系為AM＝(　?? 　)DE；

②如圖3，當(dāng)∠BAC＝120°，ED＝6時(shí)，AM的長為(　?? 　)．

（2）猜想論證：

在圖1中，當(dāng)∠BAC為任意角時(shí)，猜想AM與DE之間的數(shù)量關(guān)系，并給予證明．

（3）拓展應(yīng)用

如圖4，在四邊形ABCD中，AD＝AB，CD＝BC，∠B＝90°，∠A＝60°，CD＝，在四邊ABCD的內(nèi)部找到點(diǎn)P，使得△PAD與△PBC互為“頂補(bǔ)等腰三角形”．并回答下列問題．

①請(qǐng)?jiān)趫D中標(biāo)出點(diǎn)P的位置，并描述出該點(diǎn)的位置為(　?? 　)；

②直接寫出△PBC的“頂心距”的長為(　?? 　)．

26．（9分）（1）發(fā)現(xiàn)：如圖1，點(diǎn)A為線段BC外一動(dòng)點(diǎn)，且BC＝a，AB＝b且填空：當(dāng)點(diǎn)A位于(　?? 　）時(shí)，線段AC的長取得最大值，且最大值為(　?? 　)（用含a、b的式子表示）．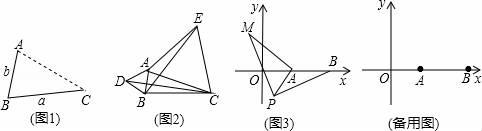

（2）應(yīng)用：點(diǎn)A為線段BC外一動(dòng)點(diǎn)，且BC＝4，AB＝2，如圖2所示，分別以AB，AC為邊，作等邊三解形ABD和等邊三角形ACE，連接CD，BE．①請(qǐng)找出圖中與BE相等的線段，并說明理由；?? ②直接寫出線段BE長的最大值．

（3）拓展：如圖3，在平面直角坐標(biāo)系中，點(diǎn)A的坐標(biāo)為（2，0），點(diǎn)B的坐標(biāo)為（5，0），點(diǎn)P為線段AB外一動(dòng)點(diǎn)，且PA＝2，PM＝PB，∠BPM＝90°，請(qǐng)直接寫出線段AM長的最大值及此時(shí)點(diǎn)P的坐標(biāo)．

參考答案

一、選擇題：本大題共10小題，每題3分，共30分．

1．D．2．D．3．C．4．B．5．A．

6．B．7．D．8．B．9．C．10．D．

二、填空題：本大題共7小題，每題4分，共28分．把你的答案填入答題紙中相應(yīng)的位置上．

11．（2，3）．12．40°．13．答案：12．

14．0?? 15．180°﹣2α? 16．14．17．﹣2．

三、解答題：本大題共9小題，共62分．

18．解：（1）原式＝18x3y；

（2）原式＝a2﹣4b2；

（3）原式＝a6﹣a6﹣4a6＝﹣4a6；

（4）原式＝（x3y2﹣x2y﹣x2y+x3y2）÷3x2y

＝（2x3y2﹣2x2y）÷3x2y

＝xy﹣．

19．解：（1）a2b+ab2＝ab（a+b）；

（2）ab2﹣4ab+4a＝a（b2﹣4b+4）＝a（b﹣2）2；

（3）x2（a﹣b）+y2（b﹣a）＝（a﹣b）（x2﹣y2）＝（a﹣b）（x+y）（x﹣y）．

20．解：△OEF的形狀為等腰三角形．

理由如下：∵BE＝CF，

∴BE+EF＝CF+EF，即BF＝CE．

在△ABF與△DCE中，

．

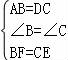∴△ABF≌△DCE（SAS）．

∴∠AFB＝∠DEC．

∴OE＝OF，即△OEF的形狀為等腰三角形．

21．解：原式＝x2﹣9+4x2﹣4x+1﹣4x2+4x＝x2﹣8，

當(dāng)x＝根號(hào)7時(shí)，原式＝7﹣8＝﹣1．

22．解：（1）△A′B′C′即為所求；

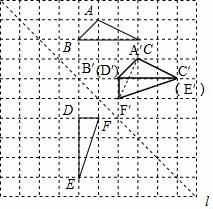
（2）△D′E′F′即為所求；

（3）45°．

23．解：（1）直線l即為所求作的直線．（見圖1）

（2）①45°≤∠ABC＜90°．

理由如下：連接AC，

當(dāng)∠ACB≤90°時(shí)垂足E在線段BC上，

∵CD垂直平分AB，

∴CA＝CB，

∴∠CAB＝∠CBA，

∵2∠CBA+∠ACB＝180°，

∴2∠CBA≥90°

∴∠CBA≥45°

∵∠CBA是銳角，

∴45°≤∠CBA＜90°

②在圖2中，

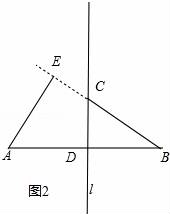
證明：∵線段AB的垂直平分線為l，

∴CD⊥AB，

∵AE⊥BE，

∴∠AEB＝∠BDC＝90°，

∴∠BAE+∠B＝∠BCD+∠B＝90°，

∴∠BAE＝∠BCD．

24．（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc．

（2）30；

（4）156．

25．解：（1）2分之1

②3

（2）猜想：結(jié)論AM＝2分之1DE．

理由如下：如圖，過點(diǎn)A作AN⊥ED于N

∵AE＝AD，AN⊥ED

∴∠DAN＝2分之1∠DAE，ND＝2分之1DE

同理可得：∠CAM＝2分之1∠CAB，

∵∠DAE+∠CAB＝180°，

∴∠DAN+∠CAM＝90°，

∵∠CAM+∠C＝90°

∴∠DAN＝∠C，

∵AM⊥BC

∴∠AMC＝∠AND＝90°

在△AND與△AMC中，

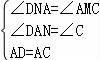
∴△AND≌△AMC（AAS），

∴ND＝AM

∴AM＝2分之1DE

（3）①線段BC的垂直平分線交AC于點(diǎn)P，

②2分之根號(hào)3

解：（1）CB的延長線上，a+b；

（2）①CD＝BE，

理由：∵△ABD與△ACE是等邊三角形，

∴AD＝AB，AC＝AE，∠BAD＝∠CAE＝60°，

∴∠BAD+∠BAC＝∠CAE+∠BAC，

即∠CAD＝∠EAB，

在△CAD與△EAB中，

，

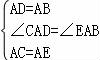∴△CAD≌△EAB，

∴CD＝BE；

②∵線段BE長的最大值＝線段CD的最大值，

由（1）知，當(dāng)線段CD的長取得最大值時(shí)，點(diǎn)D在CB的延長線上，

∴最大值為BD+BC＝AB+BC＝6；

（3）連接BM，∵將△APM繞著點(diǎn)P順時(shí)針旋轉(zhuǎn)90°得到△PBN，連接AN，

則△APN是等腰直角三角形，

∴PN＝PA＝2，BN＝AM，

∵A的坐標(biāo)為（2，0），點(diǎn)B的坐標(biāo)為（5，0），

∴OA＝2，OB＝5，

∴AB＝3，

∴線段AM長的最大值＝線段BN長的最大值，

∴當(dāng)N在線段BA的延長線時(shí)，線段BN取得最大值，

最大值＝AB+AN，

∵AN＝根號(hào)2AP＝2根號(hào)2，

∴最大值為2 根號(hào)2+3；

如圖2，過P作PE⊥x軸于E，

∵△APN是等腰直角三角形，

∴PE＝AE＝根號(hào)2，

∴OE＝BO﹣AB﹣AE＝5﹣3﹣根號(hào)2＝2﹣根號(hào)2，

∴P（2﹣根號(hào)2，根號(hào)2）．

如圖3中，根據(jù)對(duì)稱性可知當(dāng)點(diǎn)P在第四象限時(shí)，P（2﹣根號(hào)2，﹣根號(hào)2）時(shí)，也滿足條件．

綜上所述，滿足條件的點(diǎn)P坐標(biāo)（2﹣根號(hào)2，根號(hào)2）或（2﹣根號(hào)2，﹣根號(hào)2），AM的最大值為2+3．